Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 34
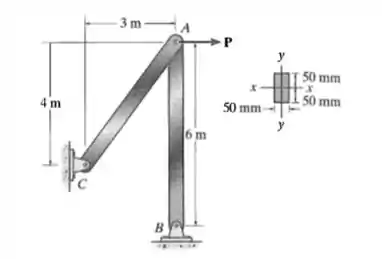
Determine a carga máxima que a estrutura pode suportar sem provocar flambagem no elemento estrutural . Considere que AB é feito de aço e que suas extremidades estão presas por pinos para flambagem no eixo e engastadas em ambas as extremidades para flambagem no eixo ., .
Passo 1
Falaaa! Queremos a carga máxima que não causa flambagem na nossa coluna . Basicamente vamos achar a carga na nossa coluna em função de e comparar com as cargas críticas da flambagem para descobrir .
Lembrando que para o aço, .
Primeiro, vamos fazer o DCL dessa estrutura:
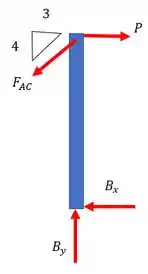
Passo 2
Agora, vamos determinar a carga na barra AB em função de ;
Pelo equilíbrio de forças em :
Passo 3
Precisamos comparar essa força em com as cargas críticas de flambagem. Então vamos calculá-las! E como essas cargas são as cargas máximas que nossa haste pode suportar sem flambar, podemos igualar
E descobrir .
Vamos então, usar a fórmula da carga crítica para a flambagem:
Normalmente, só calculamos em relação ao menor. Mas como a haste tem condições diferentes de apoio para cada caso, vamos calcular esse carga para cada caso, tá bem?
Para todos esses casos, vamos ter:
Passo 4
Vamos olhar o caso onde nossa haste pode flambar em torno de . Nesse caso, ela está presa por pinos, então .
O momento de inércia fica:
E agora, substituindo os valores numéricos pertencentes a cada variável, lembrando que é o comprimento da haste, chegamos até:
Passo 5
Agora para o caso onde ela pode flambar em torno de , como ela está engastada nas duas pontas, temos .
O momento de inércia fica:
E agora, substituindo os valores numéricos pertencentes a cada variável, lembrando que é o comprimento da haste, chegamos até:
Escolhemos então o menor valor de que a gente achou.
Passo 6
Com isso, vamos substituir na fórmula tensão crítica para comparamos com o valor dado e saber se não há escoamento do material para essa carga em :
OK!
Ufa! Terminamos!