Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 10
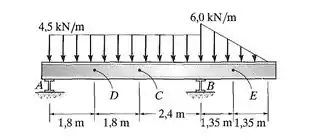
A viga suporta a carga distribuída mostrada. Determine as cargas internas resultantes na seção transversal que passa pelo ponto C. Considere que as reações nos apoios A e B sejam verticais.
Passo 1
Em um primeiro passo, vamos fazer o DCL, multiplicando as forças pela distância em que elas atuam. Temos:
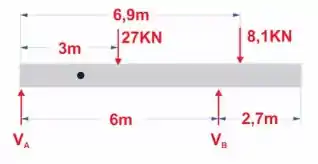
Onde Força cortante em B
Força cortante em A
Passo 2
Depois, vamos usar as equações de equilíbrio e momento
Passo 3
Agora, vamos repetir o primeiro passo, porém apenas para o segmento AC
Passo 4
Novamente, vamos usar as equações de equilíbrio e momento
Resposta
Exercícios de Livros Relacionados
Represente graficamente os diagramas de força cortante e momento fletor para a viga.
Represente graficamente os diagramas de força cortante e momento fletor para a viga e determine a força cortante e o momento em função de x .
Determine o torque resultante interno que age sobre as seções transversais nos pontos C e D do eixo. O eixo está preso em B.
Determine a força normal interna resultante que age na seção transversal no ponto A em cada coluna. Em (a), o segmento B C tem massa de 300k g / m e o segmento C D tem massa de 400k g / m . Em (b ), a
Determine o torque resultante interno que age nas seções transversais nos pontos B e C .