Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 30
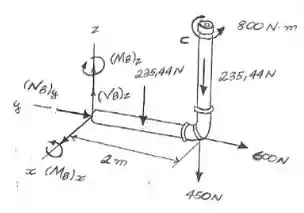
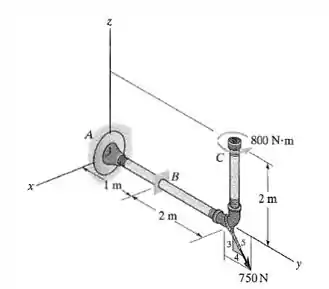
O cano tem massa de 12 kg/m e está preso à parede em A. Determine as cargas internas resultantes que agem na seção transversal que passa por B.
Passo 1
Primeiramente, devemos determinar as forças atuantes na seção B do cano. Para isso, faremos um corte na seção, transportando os esforços para ela. Desenhando o DLC, temos:
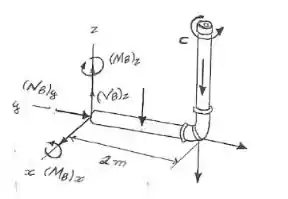
As forças verticais representam o peso distribuído no cano.
Podemos ver que não há forças na direção x. Decompondo-se a força de 750N nas direções y e z, obtemos, respectivamente:
N
N
Além disso, temos que o peso do cano é 12kg/m, logo, como temos 2 metros de cano em y e 2 metros em z, teremos duas forças de Repare que a parte de 1 metro não entra no cálculo, pois os esforços nas seções são calculados por um lado ou pelo outro.
Fazendo o somatório das forças nas direções:
Passo 2
Vamos agoira determinar os momentos atuantes em B. Primeiramente temos um momento fletor na direção z que já é dado no problema:
Basta calcular o momento fletor em x e o torsor em y. Sabemos que o momento é a força vezes o braço de alavanca (distância até o ponto).
Repare que não há momento torsor, pois não há um momento em torno que tende ao giro em torno de y.
Desenhando-se o diagrama de corpo livre com as forças calculadas, ficamos com:
