Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 31
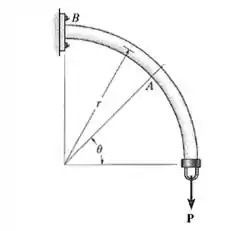
A haste curvada tem raio r e está presa em B. Determine as cargas internas resultantes que agem na seção transversal que passa pelo ponto A, o qual está localizado a um ângulo θ em relação à horizontal.
Passo 1
Falaa, querido! A gente quer as cargas internas na seção .
Nesse tipo de questão, o bizu é a gente cortar a nossa peça nessa seção e olhar só para o lado dela que a gente já tem todas as informações (todas as forças atuando), posicionar as componentes dos esforços internos nela, achar eles pelas equações de equilíbrio.
Vamos fazer isso!
Primeiramente, vamos desenhar o diagrama de corpo livre para vizualizar melhor a situação. A gente vai olhar só para o lado direito onde a força é .
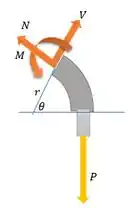
Passo 2
Vamos tratar as forças normais a seção A como o eixo x e as forças paralelas à seção como eixo y.
A gente precisa decompor nesses eixos:
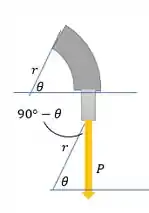
Como não temos mais nenhuma força atuante:
Passo 3
Agora vamos calcular o momento atuante em A.
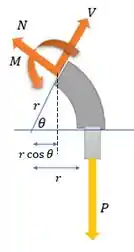
O eixo de é essa linha pontilhada. Vemos que a distância do ponto de aplicação da força a esse eixo A é .
Logo, o momento é a força vezes a distância.
Resposta
)