Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 25
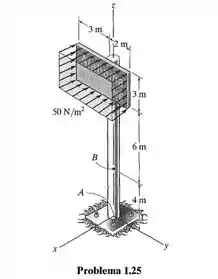
Determine as cargas internas resultantes que agem na seção transversal que passa pelo ponto do poste de sinalização. O poste está fixado ao solo, e uma pressão uniforme de age perpendicularmente à parte frontal da placa de sinalização.
Passo 1
Fala aí galerinha. Bora pra mais uma questão. A gente precisa dos esforços internos em .
A ideia para achar esforços internos em uma seção é que a gente pode cortar nossa barra nessa seção e escolher um dos pedaços.
No nosso caso, podemos escolher o lado de cima, aí não precisamos achar as reações no solo sobre nossa viga. E aí, colocamos as componentes dos esforços internos nessa seção e achamos seus valores pela equação de equilíbrio, ok?
No ponto temos cortante, normal e momentos fletor e torsor. Temos que calcular todos esses esforços na seção. Vamos fazer um DCL disso:
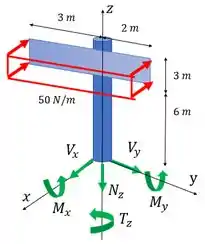
Vamos começar!
Passo 2
Vamos pegar primeiro o esforço cortante em
Como pressão é a força sobre a área, a força será a pressão vezes a área. Foi isso que fizemo ali:
Agora, vamos calcular o cortante em na barra. Ele será dado por:
Como não temos esforços em o cortante nesse sentido é nulo.
Agora vamos pegar o esforço normal:
A mesma maneira que em não temos esforço na direção o que nos dá um esforço normal nulo.
Passo 3
Agora, vamos pegar o momento. Pegando o momento fletor em
Como podemos ver, nenhuma força gera momento em o que nos dá um momento fletor nulo no eixo.
Já o momento em será dado por:
Vamos pegar o centroide da área ocupada pela pressão como ponto de atuação da força resultante produzida sobre ela. A coordenda dele é :
.
Por último, temos o momento em
Repara que a carga distribuída em cada lado da placa vai sofrer momentos em direções opostas. A placa tende a dobrar. Então, a gente precisa calcular a resultante em cada lado da placa para descobrir o momento resultante.
Aí cada lado terá a sua coordenada do centroide em relação ao eixo , onde se localiza a sua respectiva resultante:
Prontinho galera.