Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 2.Problemas - Ex. 16
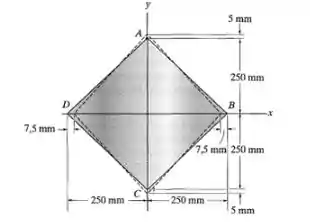
Os cantos da chapa quadrada sofrem os deslocamentos indicados. Determine a deformação por cisalhamento ao longo das bordas da chapa em A e B.
Passo 1
Primeiramente, vamos representar a situação:
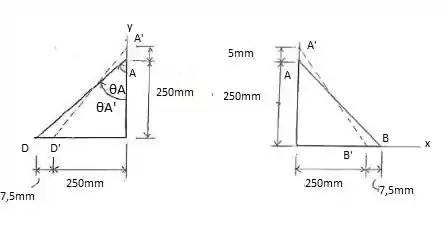
Podemos calcular os ângulos utilizando as seguintes relações:
-1
-1
-1
-1
Passo 2
Podemos agora calcular as deformações, tomando o cuidado de tranformar os ângulos para radiano:
Resposta
Exercícios de Livros Relacionados
3. As componentes do estado plano de deformação no ponto sobre a aba do pino são ϵ x = ( 200 × 10 - 6 ) , ϵ y = ( 180 × 10 - 6 ) e γ x y = ( - 300 × 10 - 6 ) . Use as equações de transformação da defo
As componentes do estado plano de deformação no ponto da aba da bequilha são ϵ x = ( - 400 × 10 - 6 ) , ϵ y = ( 860 × 10 - 6 ) e γ x y = ( 375 × 10 - 6 ) . Use as equações de transformação da deformaç
4. Resolva o Problema 10.3 para um elemento orientado a um ângulo θ = 30 ° em sentido horário.
Devido à carga P, as componentes do estado plano de deformação no ponto do suporte são ϵ x = ( 500 × 10 - 6 ) , ϵ y = ( 350 × 10 - 6 ) e γ x y = ( - 430 × 10 - 6 ) . Use as equações de transformação d
6. As componentes do estado plano de deformação no ponto sobre uma chave são ϵ x = ( 120 × 10 - 6 ) , ϵ y = ( - 180 × 10 - 6 ) e γ x y = ( 150 × 10 - 6 ). Use as equações de transformação da deformaçã