Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 39

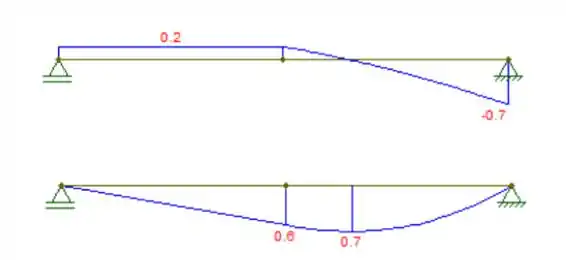
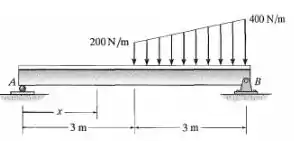
Represente graficamente os diagramas de força cortante e momento fletor para a viga e determine a força cortante e o momento em função de x .

Passo 1

Primeiramente, devemos calcular as reações de apoio utilizando as equações da estática:

∑ M a = 0 → - 600 × 4,5 - 300 × 5 + 3 F b = 0

F b = 700 N

∑ F y = 0 → F a + 700 - 400 + 200 × 1,5 = 0

F a = 200 N

Passo 2

Com as reações calculadas, podemos fazer os respectivos diagramas de cortante e de momento fletor:

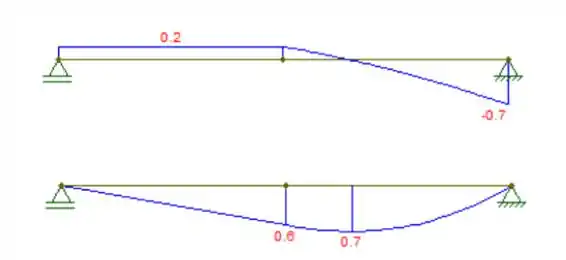
Passo 3

O problema nos pede a equação dos esforços, para isso, devemos separar a viga em 2 trechos:

Trecho 1 1 < x < 3 :

V x = 200 N

M x = 200 x

Trecho 2 3 < x < 6 :

V x = - 100 3 x ² + 500

M x = - 100 9 x ³ + 500 x - 600

Resposta

Trecho 1 1 < x < 3 :

V x = 200 N

M x = 200 x

Trecho 2 3 < x < 6 :

V x = - 100 3 x ² + 500

M x = - 100 9 x ³ + 500 x - 600

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o torque resultante interno que age nas seções transversais nos pontos B e C .
O dispositivo mostrado na figura sustenta uma força de 80N . Determine as cargas internas resultantes que agem sobre a seção no ponto A .
Determine as cargas internas resultantes que agem na seção transversal no ponto D do elemento AB.
Resolva o Problema 1.6 para as cargas internas resultantes que agem no ponto E.
A viga AB é suportada por um pino em A e por um cabo BC. Determine as cargas internas resultantes que agem na seção transversal no ponto D.