Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 9

Represente graficamente os diagramas de força cortante e momento fletor para a viga. Dica: A carga de 100 kN deve ser substituída por cargas equivaletes no ponto C no eixo da viga.

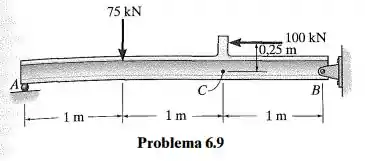
Passo 1

Fazemos o diagrama de corpo livre e e usamos as equações de equilíbrio

∑ F x = 0 ⇒ - 100 + R B X = 0

R B X = 100   k N

∑ M B = 0 ⇒ - R A ⋅ 3 + 75 ⋅ 2 + 100 ⋅ 0,25 = 0

R A = 58,33   k N

∑ F Y = 0 ⇒ R A - 75 + R B = 0

R B = 16,67   k N

Passo 2

Vamos substituir a carga excêntrica por uma carga equivalente em C

∑ M = 0 ⇒ M C - 100 ⋅ 0,25 = 0

M C = 25   k N m

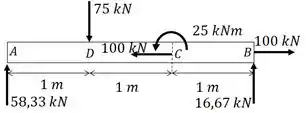
Passo 3

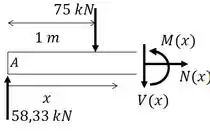
Fazendo uma seção ente AD 0 ≤ x < 1   m :

∑ F x = 0 ⇒ N x = 0

∑ F Y = 0 ⇒ 58,33 - V ( x ) = 0

V ( x ) = 58,33   k N

∑ M = 0 ⇒ - 58,33 ⋅ x + M x = 0

M x = 58,33 x

Fazendo uma seção ente DC 1 ≤ x < 2   m :

∑ F x = 0 ⇒ N x = 0

∑ F Y = 0 ⇒ 58,33 - 75 - V ( x ) = 0

V x = - 16,67   k N

∑ M = 0 ⇒ - 58,33 ⋅ x + 75 x - 1 + M x = 0

M x = - 16,67 x + 75

Fazendo uma seção ente CB 2 ≤ x < 3   m :

∑ F x = 0 ⇒ N x - 100 = 0

N x = 100   k N

∑ F Y = 0 ⇒ 58,33 - 75 - V ( x ) = 0

V x = - 16,67   k N

∑ M = 0 ⇒ - 58,33 ⋅ x + 75 x - 1 + 25 + M x = 0

M x = - 16,67 x + 50

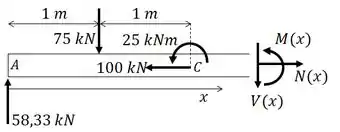
As equações são:

V x =         58,33   k N 0 ≤ x < 1 - 16,67   k N 1 ≤ x < 2 - 16,67   k N 2 ≤ x ≤ 3

M x =         58,33 x                     0 ≤ x < 1 - 16,67 x + 75 1 ≤ x < 2 - 16,67 x + 50 2 ≤ x ≤ 3

Passo 4

Utilizando as equações chegamos nos gráficos:

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O guindaste de tambores suspende o tambor de 2,5k N . O pino de ligação está conectado à chapa em A e B . A ação de aperto sobre a borda do tambor é tal que somente forças horizontais e verticais são
Determine as cargas internas resultantes que agem na seção transversal que passa pelo ponto D no Problema 1. 18.
A viga suporta a carga distribuída mostrada. Determine as cargas internas resultallles que agem na seção transversal que passa pelo ponto C . Considere que as reações nos apoios A e B sejam verticais.
A estrutura do poste de energia elétrica suporta os três cabos, e cada um deles exerce uma força de 4k N nas escoras. Se as escoras estiverem acopladas por pinos em A , B e C , determine as cargas int
Determine as cargas internas resultantes que agem na seção transversal que passa pelo ponto B .