Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 11

Represente graficamente os diagramas de força cortante e momento fletor para a viga composta. Ela é suportada por uma chapa lisa em A, que desliza no interior de uma ranhura e, por isso, não pode suportar uma força vertical, embora possa suportar momento e carca axial.

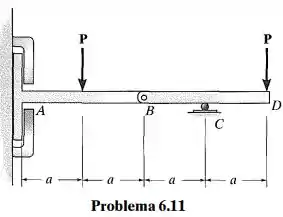
Passo 1

Desenhamos o diagrama de corpo livre e calculamos as reações de apoio.

∑ F y = 0 ⇒ - P + R C - P = 0

R C = 2 P

∑ M D = 0 ⇒ M A + P ⋅ 3 a - R C ⋅ a = 0

M A + P ⋅ 3 a - 2 P ⋅ a = 0

M A = - P ⋅ a

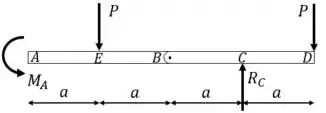
Observe que no ponto B há um pino. Vamos decompor este pino:

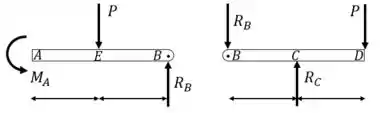
Perceba que em um pino não há esforço de momento. Isso quer dizer que no nosso gráfico de momento fletor, este será um ponto de momento igual a zero.

Passo 2

Vamos fazer sucessivas seções na viga para calcular seus esforços internos.

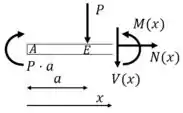
Entre AE: 0 ≤ x ≤ a

∑ F y = 0 ⇒ V x = 0

∑ M = 0 ⇒ M x - P ⋅ a = 0

M x = P ⋅ a

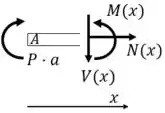
Entre EC: a ≤ x ≤ 3 a

∑ F y = 0 ⇒ - V x - P = 0

V x = - P

∑ M = 0 ⇒ M x - P ⋅ a + P ( x - a ) = 0

M x = - P x + 2 P ⋅ a

Entre CD: 3 a ≤ x ≤ 4 a

∑ F y = 0 ⇒ - V x - P + R C = 0

- V x - P + 2 P = 0

V x = P

∑ M = 0 ⇒ M x - P ⋅ a + P x - a - R C ( x - 3 a ) = 0

M x = P x - 4 P ⋅ a

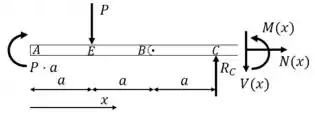
As equações são:

V x = 0 0 ≤ x ≤ a - P a ≤ x ≤ 3 a           P 3 a ≤ x ≤ 4 a

V x = P ⋅ a                           0 ≤ x ≤ a - P x + 2 P ⋅ a a ≤ x ≤ 3 a           P x - 4 P ⋅ a 3 a ≤ x ≤ 4 a

Passo 3

Com as equações podemos desenhar os gráficos:

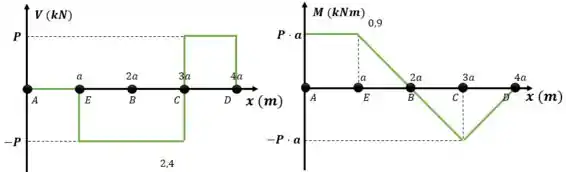
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixo está apoiado em suas extremidades por dois mancais, A e B , e está sujeito às forças aplicadas às polias nele fixadas. Determine as cargas internas resultantes que agem na seção transversal que
Determine as cargas internas resultantes que agem na seção transversal que passa pelo ponto B do poste de sinalização. O poste está fixado ao solo, e uma pressão uniforme de 50N / m ² ² age perpendicu
A viga mestra A B suporta a carga na asa do avião. As cargas consideradas são a reação da roda de 175k N em C , o peso de 6k N do combustível no tanque da asa, com centro de gravidade em D, e o peso d
O cano tem massa de 12k g / m . Se ele estiver fixado à parede em A , determine as cargas internas resultantes que agem na seção transversal em B . Despreze o peso da chave C D .
Determine as cargas internas resultantes nas seções transversais que passam pelos pontos K e J no guindaste de tambores no Problema 1. 21.