Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 9

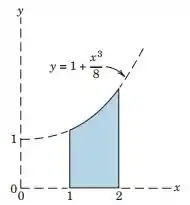
Determine the x- and y-coordinates of the centroid of the shaded area.

Passo 1

Vamos lá resolver mais essa. Para a gente descobrir as coordenadas do centroide, primeiro precisamos calcular a área embaixo da curva. Escolhendo um elemento de área dA:

d A = y d x = 1 + x 3 8 d x

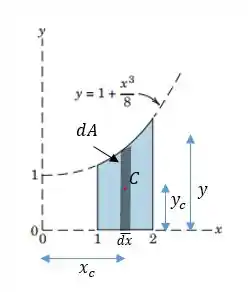
Assim, a área vai ser:

A = ∫ d A = ∫ 1 2 1 + x 3 8 d x = 2 + 2 4 32 - 1 + 1 4 32 = 47 32

Passo 2

Vamos lembrar o seguinte:

x - = ∫ x c d A A  

y - = ∫ y c d A A  

Então a gente precisa calcular as integrais antes. Para a primeira integral, temos:

∫ x c d A = ∫ 1 2 x 1 + x 3 8 d x = 2 2 2 + 2 5 40 - 1 2 2 + 1 5 40 = 91 40

Observando a figura do passo 1, temos y c = y 2 . Substituindo na segunda integral:

∫ y c d A = ∫ y 2 y d y   = 1 2 ∫ y 2 d x

∫ y c d A = 1 2 ∫ 1 2 1 + x 3 8 2 d x =   1 2 ∫ 1 2 1 + x 3 4 + x 6 12 d x

∫ y c d A = 1 2 2 + 2 4 2 + x 7 448 - 1 + 1 4 16 + 1 7 448 = 995 896

Passo 3

Com os valores das integrais, agora vamos usar esses valores para calcular as coordenadas dos centroides:

x - = ∫ x c d A A = 91 40 47 32 = 1,549

y - = ∫ y c d A A   = 995 896 47 32 = 0,756

Resposta

x - = 1,549; y - = 0,756

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as coordenadas do centroide do corpo com cinco orifícios totalmente perfurados. Cada um dos quatro pequenos orifícios tem um raio de 6m m .
Localize o centróide da área mostrada na figura por integração direta. (Cuidado: observe cuidadosamente o sinal adequado do radical envolvido.)
Determine a posição do centro de massa da casca cilíndrica com uma extremidade semicircular fechada. A casca é em chapa de metal com massa de 24k g / m 2 , e a extremidade em chapa de metal com massa
Determine as coordenadas do centro de massa do corpo homogêneo mostrado. O furo está centrado na superfície horizontal superior.
Determine as coordenadas do centroide da área sombreada.