Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 29

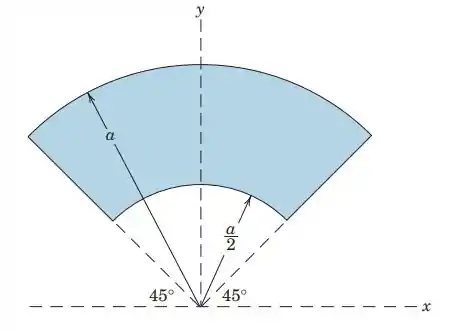
5.29. Determine the y-coordinate of the centroid of the shaded area.

Passo 1

Vamos lá, queremos descobrir o centro de massa no eixo y , e para isso vamos usar a equação

y - = ∫ y c d A A

Primeiro vamos descobrir o elemento de área d A .

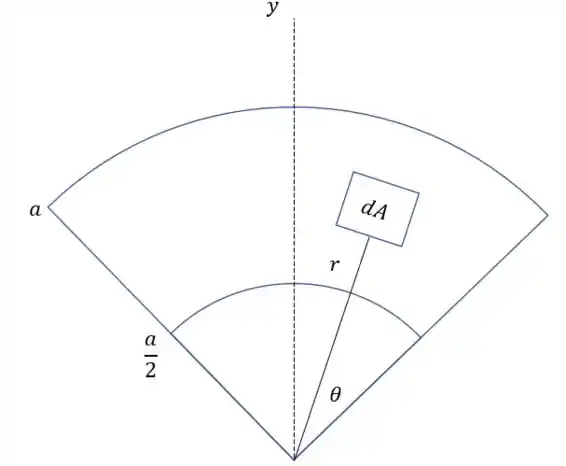
Então

d A = r   d r   d θ

E nessa imagem temos

y c = r s i n   θ

Passo 2

Agora vamos determinar a área da figura, não vai ser complicado, olha só, a imagem é 1 4 de um círculo, e sabemos que a área do círculo é A c í r c u l o = π r 2 , como r = a , a área da porção do círculo maior é

A 1 = 1 4 π a 2

Agora temos que subtrair a porção do círculo de baixo, com o raio r = a 2 , então

A 2 = 1 4 π a 2 4  

Então a área da imagem é

A = A 1 - A 2 = 1 4 π a 2 1 - 1 4 = 3 16 π a 2

Passo 3

Agora podemos montar nossa integral, que no caso vai ser uma integral dupla:

y - = ∫ ∫ y C A d A

Então

y - = ∫ ∫ r s i n   θ 3 16 π a 2 r   d r   d θ

Agora temos um problema, quais são os limites dessa integral. Bom, os limites em r a gente vê de primeira, o menor raio possível é r = a 2 e o maior raio possível é r = a , agora vamos ver como fica os limites do ângulo, olha só, vamos adotar o sentido anti-horário como positivo, então, o menor ângulo é 45 ° , e o maior ângulo vai ser 135 ° , que é o ângulo onde a figura começa somado com o ângulo da figura 90 ° Para deixar nossa conta melhor de fazer vamos colocar isso em radianos.

45 ° = π 4 135 ° = 3 π 4

Passo 4

Finalmente temos

y - = ∫ π 4 3 π 4 ∫ a 2 a r s i n   θ 3 16 π a 2 r   d r   d θ

Isso fica

y - = 16 3 π a 2 ∫ π 4 3 π 4 ∫ a 2 a r 2 sin ⁡ θ d r   d θ

Isso fica

y - = 16 3 π a 2 ∫ π 4 3 π 4 sin ⁡ θ   d θ ∫ a 2 a r 2 d r  

Então

y - = 16 3 π a 2 - cos ⁡ θ π 4 3 π 4 r 2 a 2 a

Resolvendo isso ficamos com

y - = 16 3 π a 2 2 7 a 3 24

E aí vamos chegar em

y - = 14 2 9 π a

Resposta

y - = 14 2 9 π a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as coordenadas x e y do centroide da área sombreada.
O conjunto mostrado é formado por uma haste uniforme. Para qual valor do comprimento l o centro de massa estará localizado a uma altura de 3 r 4 acima da superfície de suporte?
O conjunto soldado é feito de uma haste uniforme pesando 0,370l b por pé de comprimento e a placa semicircular pesando 8l b por pé quadrado. Calcule as coordenadas do centro de gravidade da montagem.
Determine as coordenadas x , y e z do centro de massa da forma de chapa de metal mostrada.
Determine a coordenada z do centróide do sólido retangular com o orifício hemisférico. O centro do hemisfério está centrado na face superior do sólido e z é medido para cima a partir da face inferior.