Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 35

5.35. Determine the x-coordinate of the mass center of the portion of the spherical shell of uniform but small thickness.

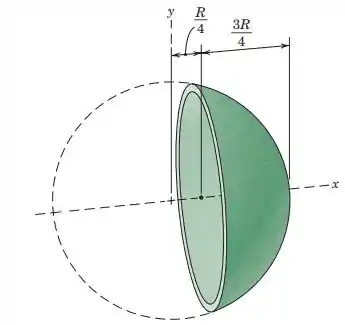
Passo 1

Vamos lá, queremos descobrir o centro de massa no eixo x , e para isso vamos usar a equação

x - = ∫ x c d m M

Primeiro vamos descobrir o elemento de área d A .

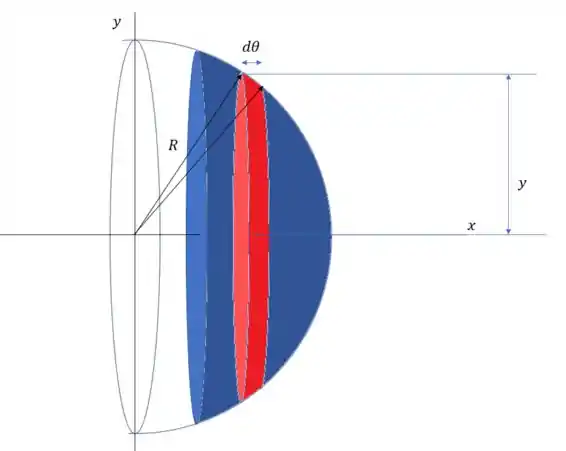
Repare que o elemento é de área e não de volume porque agora estamos estudando só uma casca.

Podemos dizer que a casca tem uma distribuição de massa homogenea. Então

d m = ρ d A

Onde ρ é a densidade.

O elemento de área é o cilindro em vermelho na figura, que tem largura

d A = 2 π y R   d θ

Em que R d θ é a largura do cilindro e 2 π y é o perimetro. Podemos usar a transformação

y = R s i n   θ

x = R c o s   θ

Então

d m = 2 π ρ R 2 sin ⁡ θ   d θ

Passo 2

Agora vamos descobrir a massa dessa figura.

M = ∫ d m

Ou seja

M = ∫ A 2 π ρ R 2 sin ⁡ θ   d θ

Vamos ver como ficam esses limites:

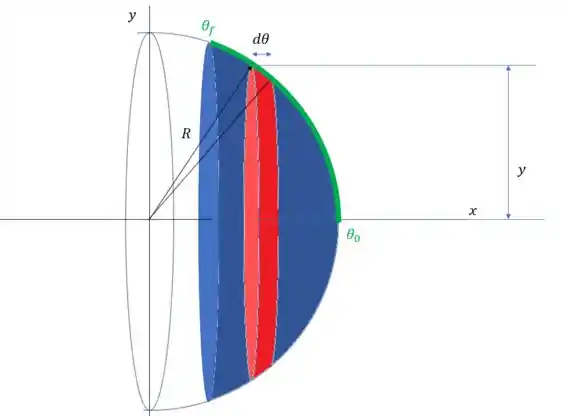
Não é complicado ver que θ 0 = 0 , agora vamos ver como fica θ f , sabemos que naquele ponto x = R 4 , isso significa que

R cos ⁡ θ = R 4

Então

θ = cos - 1 ⁡ 1 4

Então

M = ∫ 0 cos - 1 ⁡ θ 2 π ρ R 2 sin ⁡ θ   d θ  

Então temos

M = 2 π ρ R 2 - cos ⁡ θ 0 cos - 1 ⁡ θ

M = 2 π ρ R 2 - cos ⁡ ( cos - 1 ⁡ 1 4 + cos ⁡ 0

Então

M = 2 π ρ R 2 - 1 4 + 1

M = 3 2 π ρ R 2

Passo 3

Agora vamos finalmente usar a integral para descobrir a coordenada de z do centro de massa.

x - = ∫ x c d m M

Então

x - = 1 3 2 π ρ R 2 ∫ R cos ⁡ θ 2 π ρ R 2 sin ⁡ θ   d θ

Isso fica

x - = 2 R 3 ∫ 2 cos ⁡ θ sin ⁡ θ d θ

Então a nossa integral é

x - = 2 R 3 ∫ 0 cos - 1 ⁡ 1 4 sin ⁡ ( 2 θ )   d θ

Logo

x - = 2 R 3 - 1 2 cos ⁡ 2 θ 0 cos - 1 ⁡ 1 4

x - = 2 R 3 15 16 = 5 8 R

Resposta

x - = 5 8 R

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a coordenada z do centróide do sólido retangular com o segmento esférico (menos de um hemisfério) removido. O centro do hemisfério do qual o segmento é uma porção está localizado a uma distâ
Determine as coordenadas do centro de massa da montagem soldada de hastes delgadas uniformes feitas do mesmo estoque de barras.
5.50. Determine the y-coordinate of the centroid of the shaded area.
5.52. Calculate the y-coordinate of the centroid of the shaded area.
5.49. Determine the coordinates of the centroid of the trapezoidal area shown.