Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 7
Determine the y-coordinate of the centroid of the shaded area. Check your result for the special case a = 0.
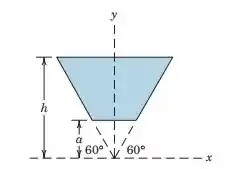
Passo 1
Vamos lá resolver mais essa. Temos que calcular a coordenada y do centroide. Para isso, temos que calcular a área da figura. A área da figura é dada por
De acordo com a figura abaixo,
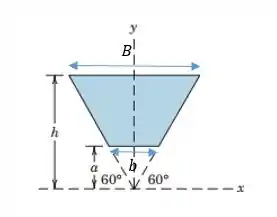
As bases podem ser calculadas como:
A área da figura é:
Passo 2
Vamos lembrar que a coordenada y do centroide é calculada por
Assim, ainda precisamos determinar o elemento de área para calcular a integral.
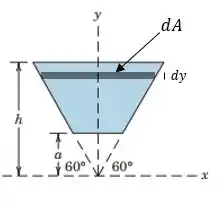
O elemento de área é dado por:
em que 2x é a base e dy é a altura do elemento de área. Agora, a gente precisa saber a função da curva que relaciona y e x. Considerando que a metade do triângulo é um triângulo retângulo, a gente pode dizer que:
Assim,
Aqui é preciso colocar tudo em função de y para calcular a integral.
Passo 3
Agora vamos calcular a integral . Como y na figura vai de até , a gente calcula como integral definida.
Substituindo na equação do centroide:
Esse é o centroide da área pintada. Para o caso especial :
Vocês podem observar depois que para o caso especial, a coordenada y do centroide é igual ao do triângulo.