Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas - Ex. 48

Determine o centróide da em z da figura abaixo.

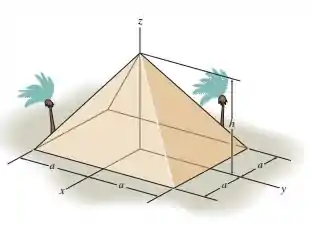
Passo 1

Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.

Primeiramente, vamos analisar a seção planificada em y z :

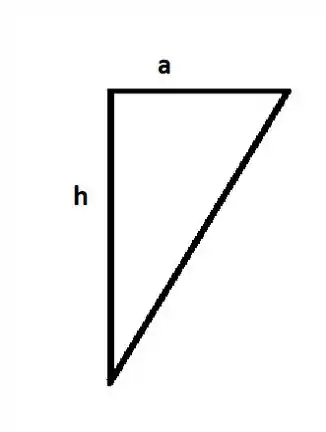
Agora, basta usar a fórmula do centroide, que é dividir a figura em outras conhecidas e fazer a média dos centroides ponderada pelas áreas:

z = ((a h)/(2) xx (2)/(3) h)/((a h)/(2)) = (2)/(3 h)

Pegando na outra direção:

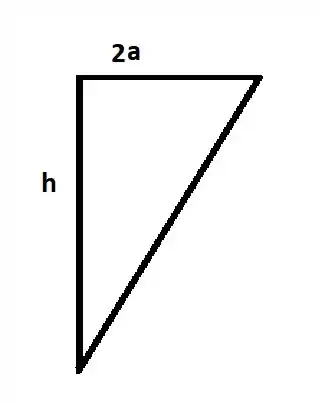
Aplicando a fórmula:

z = (2)/(3) h

Portanto, o centroide será:

z = ((2)/(3) h xx (a h)/(2) + (2)/(3) h xx (2 a h)/(2))/((a h)/(2) + (2 a h)/(2)) = ((a h^2)/(3) + (2 a h^2)/(6))/((3 a h)/(2)) = (2)/(3) a h^2 xx (2)/(3 a h) = (4 h)/(6) = (h)/(3)

Prontinho, este é o centroide na direção z .

Resposta

z = (h)/(3)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

With your pencil, make a dot on the position of your best visual estimate of the centroid of the area of the circular sector. Check your estimate by using the results of Sample Problem 5/3.
Specify the x-, y-, and z-coordinates of the mass center of the homogeneous semicylinder.
With your pencil, make a dot on the position of your best visual estimate of the centroid of the triangular area. Check the position of your estimate by referring to the results of Sample Problem 5/2
Determine the y-coordinate of the centroid of the shaded area. Check your result for the special case a = 0.
Determine the x- and y-coordinates of the centroid of the shaded area.