Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 3
Specify the x-, y-, and z-coordinates of the mass center of the homogeneous semicylinder.
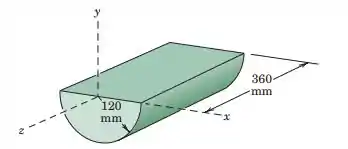
Passo 1
Vamos lá resolver mais essa. Precisamos determinar as coordenadas x, y e z do semicilindro. Você observa que o semicilindro, no plano xz, é um retângulo. Assim, o centroide fica no centro desse retângulo. Com isso, temos:
Passo 2
Agora vamos descobrir a coordena y do centroide. Para essa coordenada, a gente tem que calcular o centroide de um semicírculo, porque o centroide de um semicírculo fica no eixo y. Assim,
O sinal negativo é para indicar que está no sentido negativo do eixo.
Resposta
= 0; = -50,9 mm; = 180 mm.
Exercícios de Livros Relacionados
5.30. Determine the z-coordinate of the centroid of the volume generated by revolving the shaded area around the z-axis through 360°.
5.31. The figure represents a flat piece of sheet metal symmetrical about axis A-A and having a parabolic upper boundary. Choose your own coordinates and calculate the distance from the base to the ce
5.25. Use the results of Sample Problem 5/3 to compute the coordinates of the mass center of the portion of the solid homogeneous cylinder shown.
5.27. If the shaded area of Prob. 5/26 is rotated about the y-axis, determine the y-coordinate of the centroid of the resulting volume.
5.28. Determine the x- and y-coordinates of the centroid of the shaded area.