Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 112
Determine a componente projetada da força que atua ao longo do tubo Expresse o resultado como um vetor cartesiano.
Passo 1
Falaa, aí! Queremos projetar a força no tubo e achar sua forma vetorial. Falou de projetar, cê lembra logo de produto escalar!
Como aqui a gente está em 3D, fica mais tranquilo usarmos formulação de vetor cartesiano, tá bem?
Então, a gente precisa escrever a força como um vetor e o eixo que passa pelo tubo como vetor unitário e fazer o produto escalar entre eles.
Vem ver como fica!
Passo 2
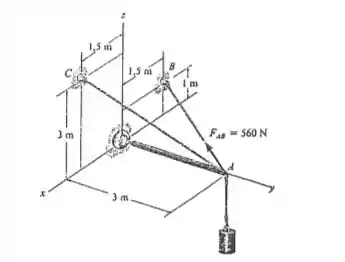
Da figura do enunciado, vamos tirar as componentes da força. Pra isso, vamos seguir um passo-a-passo.
Primeiro, vamos achar um vetor unitário no sentido da nossa força. Como a gente faz isso?
Repara que ela está na direção do cabo que sai de e vai para . Um vetor nesse sentido seria
Aí a gente acha as coordenadas desses pontos pela figura:
E calcula o vetor:
Mas lembra, a gente quer o vetor unitário, então, o próximo passo é dividir esse vetor que a gente achou pelo módulo dele:
Aí para achar o vetor da força de nessa direção é só a gente multiplicar esse vetor unitário que está na direção e sentido da nossa força pelo módulo da força:
Achamos um vetor!
Passo 3
Para achar o vetor na direção do tubo, vamos fazer basicamente a mesma coisa. Podemos dizer que nossa direção sai de e vai para .
Nosso vetor vai ser
Maas a gente quer o vetor unitário, então:
Passo 4
Agora que a gente tem o vetor da força e o vetor unitário na direção do tubo, a gente acha a intensidade da força projetada no tubo fazendo o produto escalar entre esses vetores:
Isso é o módulo da projeção da nossa força ao longo da direção .
Para achar a forma vetorial dessa projeção, basta multiplicamos por um vetor unitário na direção. Nossa projeção da força está na direção do tubo, lembra?
Então nosso vetor unitário é aquele que a gente já tinha achado :
Prontinho!