Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 4.Problemas Fundamentais - Ex. 14

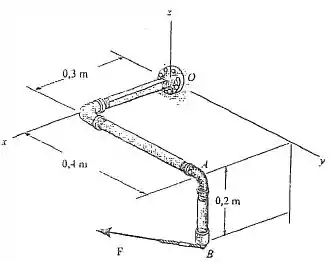
14. Determine a intensidade do momento da força F → = 300 i - 200 j + 150 k   N em relação ao eixo AO. Expresse o resultado como vetor cartesiano.

Passo 1

Para fornecer o resultado como o enunciado pede precisamos calcular o momento da força F usando o produto vetorial que é dado da seguinte maneira:

M 0 = u a → ⋅ ( r → × F → ) = u a x u a y u a z r x r y r z F x F y F z

Onde:

u a x ,   u a y   e   u a z representam as componentes do vetor unitário definido na direção do eixo de rotação

r x ,   r y   e   r z representam as coordenadas do vetor posição definido a partir de qualquer ponto O sobre o eixo de rotação até qualquer ponto na linha de aplicação da força.

F x ,   F y   e   F z são as componentes da força F aplicada.

O vetor r → mencionado acima pode ser visto na figura abaixo.

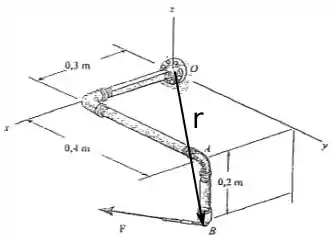
Para saber as coordenadas desse vetor, basta olhar a figura e ver quanto você tem que andar para cada direção para chegar ao ponto na linha de ação da força, logo:

r → = { 0,3 i + 0,4 j - 0,2 k }

O vetor unitário que tem a mesma direção que o eixo de rotação que é o eixo OA, é dado por:

u → = r O → r O →

Onde r O → é o vetor que sai do ponto O até o ponto A. Assim:

r O → = { 0,3 i + 0,4 j + 0 k }

r O → = 0,3 2 + 0,4 2 + 0 2

= 0,09 + 0,16

0,25 = 0,5

Logo:

u → = 0,3 i + 0,4 j + 0 k 0,5

= { 0,6 i + 0,8 j + 0 k }

Passo 2

Agora que já temos tudo que precisamos, vamos calcular o momento em relação ao eixo pedido.

M 0 = u → ⋅ ( r → × F → ) = u x u y u z r x r y r z F x F y F z

= 0,6 0,8 0 0,3 0,4 - 0,2 300 - 200 150

= 0,6 0,4 ⋅ 150 - 0,2 ⋅ 200 - 0,8 0,3 ⋅ 150 - - 0,2 ⋅ 300 + 0 - 200 ⋅ 0,3 - 0,4 ⋅ 300

= 0,6 ( 60 - 40 ) - 0,8 ( 45 + 60 ) + 0

= 0,6 ( 20 ) - 0,8 ( 105 ) + 0

= 12 - 84 = - 72   N ⋅ m

Mas isso que encontramos é a intensidade do momento, para achar ele em forma cartesiana, basta multiplicá-lo pelo vetor unitário, já que eles têm a mesma direção e sentido, assim:

M 0 → = M 0 u → = - 72 ( 0,6 i + 0,8 j + 0 k )

= ( - 43,2 i - 57,6 j + 0 k )

Resposta

A intensidade do momento da força em relação ao eixo x é:

M 0 = - 72   N ⋅ m

Expresso de forma cartesiana:

M 0 → = ( - 43,2 i - 57,6 j + 0 k )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A laje da construção está sujeita a quatro cargas paralelas das colunas. Determine a força resultante equivalente e especifique sua posição x ,y sobre a laje. Considere F 1 = 30k N e F 2 = 40k N .
Três forças paralelas do parafuso atuam sobre a chapa circular. Se a força em A possui uma intensidade F A = 1000N , determine as intensidades de F B e F C de modo que a força resultante F R do sistem
Determine as coordenadas do ponto no plano x z pelo qual passa a linha de ação da resultante do sistema de forças, para o sistema de forças do Prob. 2/149.
A resultante das duas forças e do torque pode ser representada por um torçor. Determine a expressão vetorial para o momento M do torçor e encontre as coordenadas do ponto P no plano x z pelo qual pass
Na posição mostrada, o virabrequim de um pequeno compressor de dois cilindros está submetido a forças de 400 N e 800 N, exercidas pelas bielas, e um torque de 200 N.m. Substitua esse sistema de carreg