Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 47
O semicilindro de 10 N apoia o bloco que tem um peso específico Determine a altura h do bloco que produzirá equilíbrio indiferente na posição mostrada.
Passo 1
Desenhando o diagrama do corpo livre: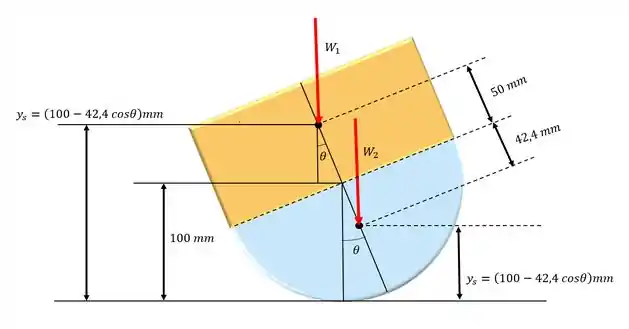
Passo 2
O primeiro passo é calcular a distância do centro de gravidade do hemisfério até a base do bloco:
Passo 3
Podemos encontrar a expressão para a energia potencial do sistema:
Passo 4
Para acharmos a posição de equilíbrio, devemos encontrar a primeira derivada da função potencial:
Passo 5
Para verificar a estabilidade, devemos calcular a segunda derivada da função potencial:
Resposta
Exercícios de Livros Relacionados
Mostre quer o equilíbrio é neutro no problema 10.6.
Mostre quer o equilíbrio é neutro no problema 10.1.
Usando o método da seção 10.8, resolva o probelma 10.35.
Usando o método da seção 10.8, resolva o probelma 10.31.
Usando o método da seção 10.8, resolva o probelma 10.36.