Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 89
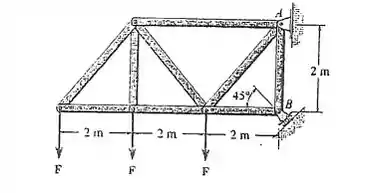
Determine as componentes horizontal e vertical da reação do pino A e a reação do rolete B necessária para suportar a estrutura. Considere F = 600 N
Passo 1
Fala ai galerinha bonita, tudo beleza?
Saca só, nesse exercício aqui o enunciado nos deu uma estrutura suportada por um pino em um ponto e um rolete num ponto , onde essa estrutura está sujeita a ação de cargas de intensidade . Então se a gente esboçar o diagrama de corpo livre do sistema, vamos obter:
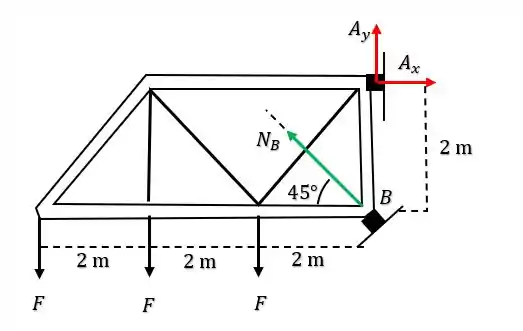
Onde é a reação normal no rolete , enquanto que e são as reações no pino .
O enunciado quer que a gente encontre justamente essas reações em cada apoio.
Belezinha, e como estamos falando de uma situação de equilíbrio, então devemos respeitar as condições:
Passo 2
Show de bolinhas, então fazendo o somatório do momento em relação ao ponto , vamos obter que:
Logo:
Portanto, a reação em é dada como:
Passo 3
Agora se a gente fizer o somatório das forças no eixo , vamos ter que:
Então isolando :
Isso quer dizer que a direção de é contraria ao que estávamos pensando inicialmente, de modo que pra gente poder escrever ela como sendo uma força positiva, podemos reescrever o diagrama de corpo livre como sendo:
Então como a gente inverteu o sentido de , teremos que:
E por fim, se a gente fizer o somatório das forças no eixo , vamos descobrir que:
Portanto:
Prontinho 😊