Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 109
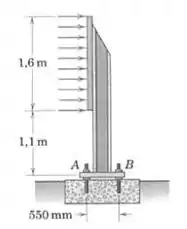
O vento soprando na direção normal ao plano da placa de sinalização retangular exerce uma pressão uniforme de , como indicado na figura. Determine as variações nas forças exercidas em e por cada apoio. Existem duas vigas em I verticais simetricamente posicionadas e a largura da placa é .
Passo 1
Podemos tratar a força associada à pressão de como se estivesse agindo no meio da placa, e o seu módulo é o seguinte:
Quando essa força age sobre a placa ela favorece que esta “tombe” para trás, ou seja, ela gera um momento que deve ser compensado na base para que a placa não vire.
Passo 2
Vamos chamar de e as variações nas forças em cada parafuso da base (são quatro no total). Como os apoios são simétricos podemos garantir que:
E juntas elas formam um binário que impede que a placa “tombe”:
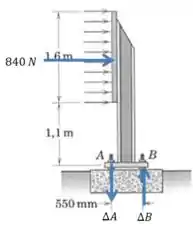
Mas essas duas variáveis são desconhecidas, então precisamos de uma equação de equilíbrio que exclua pelo menos uma delas. Vamos tomar o momento total em relação ao ponto :
Lembre que existem dois parafusos com força , e dois com força , então podemos olhar para a figura para escrever a seguinte equação para o momento:
Resposta
As variações nas forças dos suportes são .