Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 117
O guincho da ponte rolante está projetado para uma capacidade máxima de e a viga em I uniforme tem uma massa de . (a) Faça um gráfico do módulo da força no pino em em função de , ao longo da faixa de operação entre e . No mesmo sistema de eixos, faça um gráfico das componentes e da reação do pino em . (b) Determine o valor mínimo de e o valor correspondente de . (c) O pino em deve ser projetado para que valor de ? (Use )
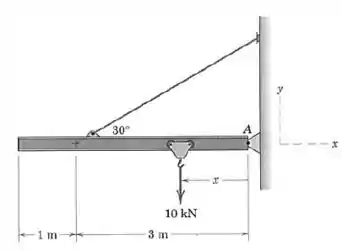
Passo 1
(a) Nosso primeiro objetivo é encontrar , e . Vamos desenhar essas e outras forças que atuam no sistema:
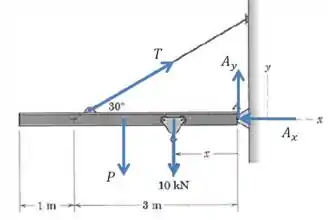
Se calcularmos o momento em relação ao ponto nós vamos excluir todas as forças desconhecidas, exceto a componente de que é perpendicular à barra:
Não esqueça de usar , conforme a orientação do enunciado.
Passo 2
Agora que encontramos uma das variáveis desconhecidas, vamos usar a condição de equilíbrio das forças para calcular e .
E agora a na direção :
Com isso já podemos escrever as funções e gráficos de , e :
Como esse problema é feito para ser resolvido no computador, nem precisamos simplificar mais essa expressão:
E agora é só jogar isso no gráfico no intervalo :
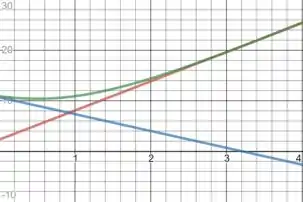
Onde a linha verde representa , a linha azul representa e a linha vermelha representa .
Passo 3
(b) Em seguida queremos encontrar o valor mínimo de , e o valor de em que isso ocorre. Lembre-se de que esse problema é feito para ser resolvido no computador.
É só dar um zoom no gráfico para encontrar o ponto de mínimo:
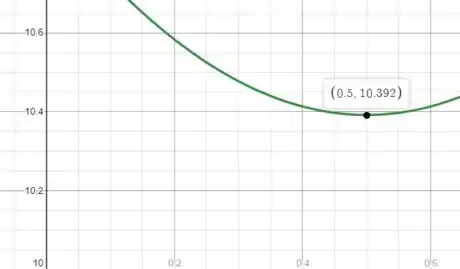
Ou seja:
Passo 4
(c) Como a faixa de operação do sistema é , o pino deve ser projetado para sustentar o caso limite, ou seja, o caso em que a força é máxima nesse intervalo
Olhando para o nosso gráfico é fácil ver que isso acontece quando também é máximo, ou seja:
Resposta
(a) Gráfico.
(b) e
(c) e .