Determine e plote, para qualquer ângulo entre pouco acima de zero e , a razão entre as forças trativas necessária para manter em equilíbrio a barra esbelta. A barra de massa é uniforme.
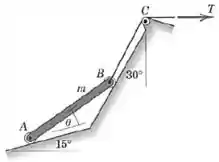
Passo 1
Vamos começar desenhando as forças que agem sobre a barra:
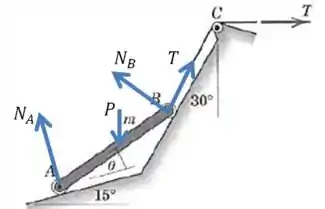
E agora podemos montar algumas equações de equilíbrio. Começando com as forças na direção vertical:
Passo 2
Agora vamos escrever a equação de equilíbrio em relação ao ponto . Nesse caso a componente da força que é perpendicular à barra é , e está a uma distância (o comprimento da barra) do ponto .
E fazendo a mesma coisa para a força , ficamos com a seguinte expressão para o momento:
E agora vamos organizar essas equações em um sistema para encontrar uma expressão para :
Queremos escrever apenas em função de e .
Passo 3
Multiplicando a primeira equação por :
E multiplicando a segunda equação por :
Agora podemos somar as duas equações para obter um resultado bem mais simples:
E o termo em parênteses é a fórmula para :
Pela terceira equação temos:
Substituindo isso na equação anterior:
E isolando :
Passo 4
Agora é só fazer o gráfico de para :
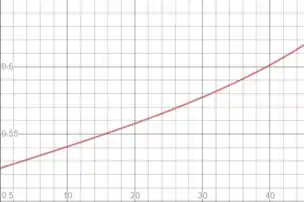
Onde o eixo é e o eixo é em graus.
Resposta
A função é .