Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 103
Uma placa de sinalização de uma auto-estrada, medindo por , é sustentada por um único poste, como mostrado. A placa, estrutura de suporte e o poste, juntos, tem uma massa de , tendo centro de massa localizado a da linha de centro vertical do poste. Quando a placa é submetida diretamente a uma lufada de vento de , uma diferença de pressão média de é desenvolvida entre as faces dianteira e traseira daplaca. Determine os módulos da força e do momento de reação na base do poste. Tais resultados seriam necessários no projeto da base.
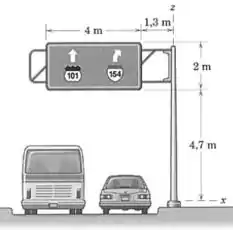
Passo 1
Podemos calcular a força resultante na base do poste apenas considerando a condição de equilíbrio das forças.
Vamos dizer que a força agindo na base tem três componentes: , e . Além dessas, quais outras forças atuam sobre o sistema? Temos o peso atuando no sentido negativo do eixo e a força associada à diferença de pressão atuando no sentido positivo do eixo :
E agora é só exigir o equilíbrio das forças em cada direção.
E então o módulo da força atuando na base do poste é:
Passo 2
Agora vamos analisar o equilíbrio dos momentos para achar o momento de reação na base do poste:
E as posições dos pontos onde as forças e agem são iguais (no centro da placa, segundo o enunciado):
E o vetor do momento na base é:
E a soma das forças:
Passo 3
Agora é só substituir tudo isso na equação principal:
E vamos escrever esse produto vetorial como um determinante:
Agora podemos calcular o módulo desse momento:
Resposta
O módulo da força é e o do momento é .