Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 6.Problemas - Ex. 102
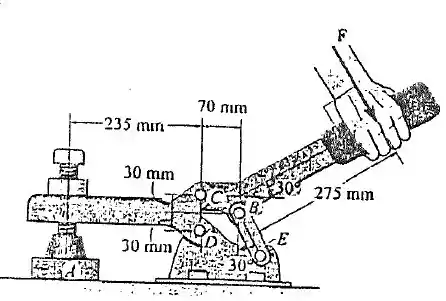
6.109. Se uma força de prensagem de é necessária em A, determine a quantidade de força F que precisa ser aplicada no cabo do grampo articulado.
Passo 1
Cara, vamos lá! Essa figura é feia, mas lutando a gente consegue! Temos um cabo acoplado em
uma estrutura que a figura mostra, através de pinos.
Desejamos encontrar a força em para que . Não dá para calcular pelas forças externas do sistema todo, porque não temos informações para isso dadas pelo enunciado.
Mas já que a estrutura tem pinos, a gente pode separa-la em duas partes, e ir resolvendo até chegar em . É isso que vamos fazer!
E onde a gente faz a separação? Onde temos pinos mesmo! Podemos soltar os pinosB, e . Fazendo isso, um diagrama da parte que contém seria
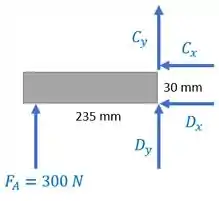
E do cabo:
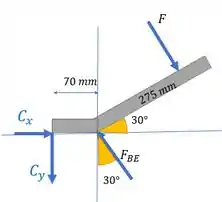
Repara que as forças que aparecem nos dois diagramas aparecem em sentidos opostos. Aí a ideia é a gente usar esses esqueminhas para achar só o que o enunciado pede. Bora!
Passo 2
Vamos começar analisando o ponto D da figura . Vamos usar que o momento total em D é 0.
Então
Passo 3
Vamos agora para a figura . Agora para o ponto C temos
Simplificando a equação temos
Agora vamos usar a equação de equilíbrio
Então
Passo 4
Agora temos duas incógnitas e duas equações
De (1) tiramos que
Substituindo em (2) temos
Então
Logo