Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 86
A balança da plataforma consiste de uma combinação de alavanas de terceira e primeira classes, de modo que a carga sobre uma alavanca se torna o esforço que move a próxima alavanca. Por meio desse arranjo, um pequeno peso pode equilibrar um objeto pesado. Se x=450 mm e a massa do contrapeso é 2kg, determine a massa da carga L necessária para manter o equilíbrio
Passo 1
Desenhando o diagrama do corpo livre do membro CD:
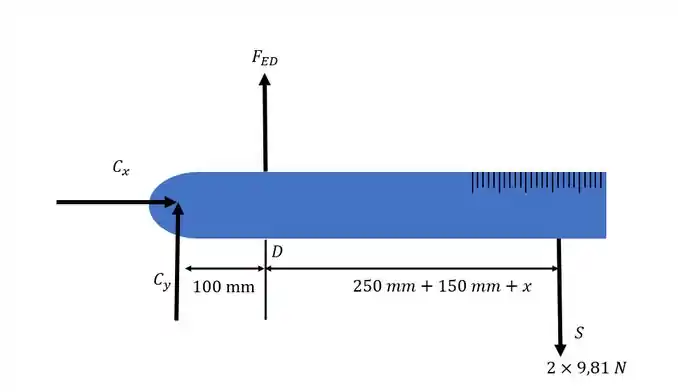
Passo 2
Usando a equação do equilíbrio em relação ao momento no ponto C:
Passo 3
Desenhando o diagrama do corpo livre do membro EG
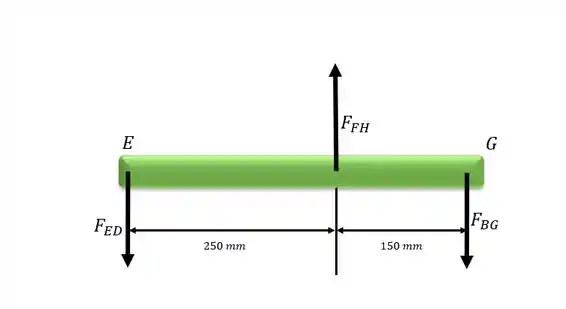
Passo 4
Usando a equação do equilíbrio em relação ao momento no ponto F:
Passo 5
Desenhando o diagrama do corpo livre do membro AB:
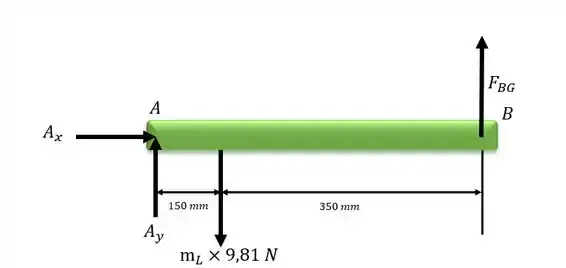
Passo 6
Usando a equação do equilíbrio em relação ao momento no ponto A:
Resposta
Exercícios de Livros Relacionados
Determine as reações no apoio fixo E e no apoio móvel A . O pino, conectado ao membro B D , atravessa um rasgo liso em D .
Um homem com peso de 875 N( ≈ 87,5 k g ) tenta se suspender usando um dos dois métodos mostrados. Determine a força total que ele precisa exercer na barra A B em cada caso e a reação normal que ele ex
Um homem com peso de 875 N( ≈ 87,5 k g ) tenta se suspender usando um dos dois métodos mostrados. Determine a força total que ele precisa exercer na barra A B em cada caso e a reação normal que ele ex
O guincho é usado para suspender o motor de 200k g . Determine a força que atua no cilindro hidráulico A B , as componentes horiozntal e vertical da força no pino C e as reações no apoio fixo D .
Dois cabos estão ligados em C e são carregados como mostra a figura. Determine a tração (a) no cabo A C e (b) no cabo B C .