Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 72
72. Determine as componentes da reação atuando nos mancais radiais lisos e .
Passo 1
Fala, querido! Queremos as reações nos mancais.
Primeiro temos que avaliar que tipos de conexões temos nessa situação, nesse caso são três mancais radiais, segundo a tabela do capítulo , seção , esse tipo de conexão por mancal radial exerce forças em duas direções.
Pelo esquema que é mostrado da situação, podemos resolver esse problema por análise escalar.
Abaixo temos um diagrama de corpo livre do nosso problema.
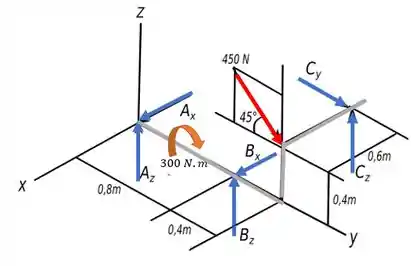
Uma observação, se encontramos alguma força negativa, isso indica que ela está no sentido oposto ao mostrado no diagrama de corpo livre.
Passo 2
Primeiro vamos usar a equação de equilíbrio da força e do momento referentes a direção , para acharmos as forças em relação ao mancal em , já que é mais simples.
Aí o momento relação a , considerando sentido anti-horário nesse eixo como positivo
Passo 3
Agora vamos usar as equações de equilíbrio de momentos referente aos outros dois eixos. Para , o sentido positivo é o anti-horário para esse eixo.
Aqui o sentido anti-horário de é positivo também:
Passo 4
Agora só no resta analisar as equações de equilíbrio referente a força nos outros dois eixos.
Já para :