Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 13

Determine as componentes da reação do engastamento em A na viga em balanço.

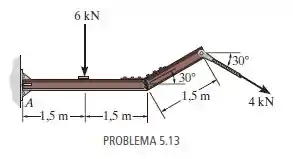
Passo 1

Aqui, temos uma viga em balanço fixa no ponto A . Para corpos em balaço, temos que as forças causam uma reação de momento. Observe o diagrama:

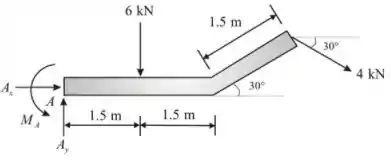
Agora você deve analisar o que seria interessante fazer para descobrir as reações.

Nós podemos aplicar o somatório de momentos em A para descobrir M A :

∑ M A = 0

M A - 6 1,5 - 4 sen ⁡ 30 ° 1,5 cos ⁡ 30 ° + 1,5 + 1,5 - 4 cos ⁡ 30 ° 1,5 sen ⁡ 30 ° = 0

M A - 9 - 8,59 - 2,59 = 0

M A = 20,18   k N

Da análise das forças em x , temos:

∑ F x = 0

A x + 4 cos ⁡ 30 ° = 0

A x = - 3,46   k N

Da análise das forças em y , temos:

∑ F y = 0

A y - 6 - 4 sen ⁡ 30 ° = 0

A y = 8   k N

Resposta

M A = 20,18   k N   ↺

A y = 8   k N ↑

A x = 3,46   k N ←

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Todos as soluções dos problemas precisam incluir um diagrama de corpo livre.F5.6. Determine as reações nos pontos de contato lisos A, B e C na alavanca.
Todos as soluções dos problemas precisam incluir um diagrama de corpo livre.F5.4. Determine as componentes da reação no engastamento A. Despreze a espessura da viga.
Todos as soluções dos problemas precisam incluir um diagrama de corpo livre.F5.3. A treliça é suportada por um pino em A e um rolete em B. Determine as reações dos apoios.
Todos as soluções dos problemas precisam incluir um diagrama de corpo livre.F5.2. Determine as componentes horizontal e vertical da reação no pino A e a reação na viga em C.
Cada corda pode admitir uma tração máxima de 500N . Determine a maior massa do tubo que pode ser suportada.