Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 3.Problemas - Ex. 35
Cada corda pode admitir uma tração máxima de . Determine a maior massa do tubo que pode ser suportada.
Passo 1
Oi pessoal? Vamos para mais um exercício?
Nos é dito que cada corda pode admitir uma tração máxima de . O exercício que a maior massa do tubo que pode ser suportada a partir dessa condição.
Analisando a corda , temos que:
Onde é o peso do tubo.
Se analisarmos agora o ponto , temos que:
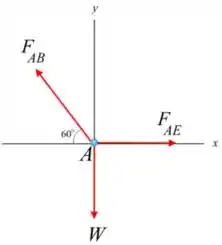
E:
Passo 2
Para o ponto , temos que:
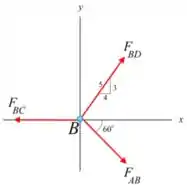
E:
Passo 3
Comparando as equações, é possível notar que a corda irá carregar o maior peso.
Portanto:
A massa do tubo será:
Resposta
Exercícios de Livros Relacionados
A viga com carga uniforme de 500 kg é submetida aos três carregamentos externos, como mostrado. Calcule as reações no pontoOdo suporte.
A massa da bicicleta é de 13 kg com centro de massa emG. Determine as forças normais emAeBquando a bicicleta está em equilíbrio.
Para testar a deflexão da viga uniforme de 100 kg, o garoto de 50 kg dá um puxão de 150 N na corda, como mostrado. Calcule a força suportada pelo pino na dobradiçaO.
Um caixote de 54k g está apoiado na porta de 27k g da caçamba de uma picape. Calcule a força trativa T em cada um dos dois cabos de sustentação, um dos quais é mostrado. Os centros de gravidade estão
É desejável que uma pessoa seja capaz de iniciar o fechamento da porta do bagageiro de uma van, desde a posição aberta mostrada, com uma força vertical P de 40N . Como um exercício de projeto, determi