Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 65
Determine a força nos membros e da treliça espacial e indique se os membros estão sob tração ou compressão. A treliça é sustentada por juntas esféricas em e ligações curtas em e .
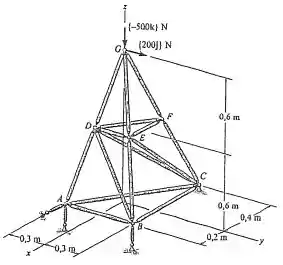
Passo 1
Para determinar as forças, deve-se fazer o diagrama de corpo livre usando o método das juntas de cada junta no qual sejam indicadas todas as forças atuando no respectivo membro.
Para esse caso não é necessário realizar a análise de todos os membros presentes, sendo possível fazer praticamente apenas a análise das juntas e por elas conterem as forças que deseja-se encontrar.
Passo 2
Escolhendo a junta primeiro e fazendo o seu DCL, tem-se que:
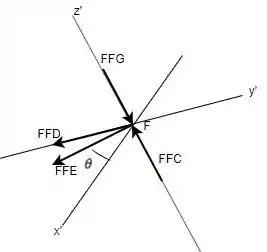
Com o DCL, podemos perceber que as forças , e estão no mesmo plano , enquanto que estão no plano .
Como é perpendicular ao plano , tem-se que:
Passo 3
Da mesma forma, fazendo o DCL da junta :
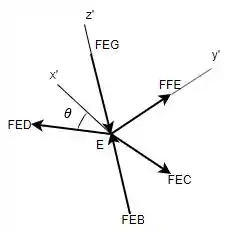
O mesmo caso de coplanaridade ocorre aqui: as forças , e estão no mesmo plano e a força é nula. Como a força está em outro plano, então: