Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 34

Determine as coordenadas do centroide por integração em termos de a e h :

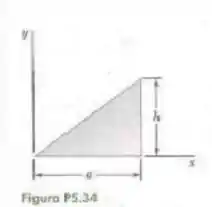
Passo 1

Fala aí galera, vamos para mais um problema de estática. O primeiro passo é determinar a relação entre x   e y . Neste caso, sabemos que:

y = K x

h = K a

k = h a

Logo:

y = h a x

x = a y h

Agora, vamos utilizar a fórmula abaixo:

x - = ∫ x d A ∫ d A  

Agora, vamos pegar um elemento retangular infinitesimal de área:

d A = y d x

Logo:

x - = ∫ x d A ∫ d A   = ∫ 0 a x y d x ∫ 0 a y d x = ∫ 0 a h a x ² ∫ 0 a h a x d x = h a 2 3 h a 2 = 2 a 3

Já para a coordenada y :

y - = ∫ y d A ∫ d A  

Onde:

d A = y d x

Logo:

y - = ∫ y 2 d A ∫ d A   = ∫ 0 a y 2 2 d x ∫ 0 a h x a d x = ∫ 0 a h 2 x 2 2 a 2 d x ∫ 0 a h x a d x = h ² a 6 a h 2 = h 3

Portanto, determinamos o centroide da figura.

Resposta

x - = 2 a 3

y - = h 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o valor do ângulo θ para que a estrutura esteja em equilíbrio:
Mostre que na medida em que r 1 se aproxima de r 2 a localização do centroide o aproxima de um arco circular de raio r 1 + r 2 2 .
Determine, para a figura da questão 5.11, a maior razão r 2 r 1 tal que y - = 3 r 1 4 .
Sabendo que d = 0 , 5 m determine o comprimento l tal que a parte B C D seja horizontal: