Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 15

Determine a deflexão no centro da viga e a inclinação em B . E I   é constante.

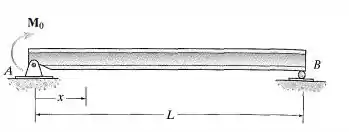
Passo 1

Para 0 ≤ x ≤ L :

∑ M = 0 M x + M 0 L x - M 0   = 0 M x = M 0 - M 0 L x

Sabemos que:

E I d 2 v 1 d x ² = M x

Logo:

E I d 2 v 1 d x 2 = M 0 - M 0 L x

E I d v 1 d x = M 0 x - M 0 2 L x 2 +   C 1

E I v = M 0 2 x 2 - M 0 6 L x 3 + C 1 x + C 2

Passo 2

As condições de contorno serão:

x = 0 → v = 0

x = L → v = 0

Logo, substituindo:

C 1 = - M 0 L 3 ; C 2 = 0

Portanto, a equação elástica será dada por:

v = M 0 6 E I L 3 L x 2 - x 3 - 2 L 2 x

Passo 3

Sabendo disso, a deflexão no centro da viga ocorre em x = L 2 . Substituindo na equação elástica: v = - M 0 L 2 16 E I

E a inclinação em B, ocorre em x = L :

θ B = M 0 L 6 E I

Resposta

v = - M 0 L 2 16 E I

θ B = M 0 L 6 E I

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma chave de torque é usada para apertar a porca de um parafuso. Se o mostrador indicar que foi aplicado um torque de 90k N . m quando o parafuso estiver totalmente apertado, determine a força P que a
As partes centrais das duas fitas métricas de madeira estão separadas por um cilindro rígido liso de 50m m de diâmetro. Determine a força F que deve ser aplicada a cada extremidade de modo que suas ex
A viga é feita de um material com peso específico y . Determine o deslocamento e a inclinação em sua extremidade A devido a seu peso. O módulo de elasticidade para o material é E .
Determine a linha elástica para a viga simplesmente apoiada utilizando a coordenada x onde 0 ≤ x ≤ L / 2 . Determine também a inclinação em A e a deflexão máxima da viga. E I é constante.
Podemos considerar que o tubo está apoiado em ambas extremidades por roletes e no centro por uma haste rígida C. A haste descansa sobre um cabo que está ligado aos apoios. Determine a força que deve s