Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 7.Problemas - Ex. 59
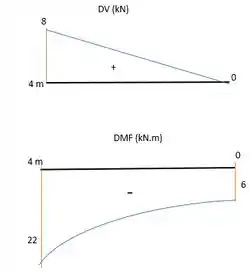
Determine os diagramas de esforço cortante e de momento fletor para a viga em balanço.
Passo 1
Fala! Essa questão é para a gente fazer os diagramas de momento e cortante dessa viga. Vamos fazer isso achando as equações desses esforços. Tem um passo a passo para fazer isso. Só seguir, que dá bom!
Primeiro, a gente repara ao olhar para viga que as equações e vão ser as mesmas para toda a viga. Isso porque não temos mudanças no carrgamento entre os apoios.
Com isso em mente, a gente se faz uma pergunta: eu consigo cortar essa viga numa seção genérica entre os apoios, olhar para um lado só, e saber todos o valor de todos os carregamentos nesse lado de cara?
Tipo, se a gente cortar nossa viga numa seção que dista da extremidade, assim e só olhar para direita:
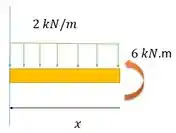
Percebe que a gente conhece todos os carregamentos? Então nossa resposta a pergunta é sim, né? E aí, algo interessante acontece. A gente nem precisa achar as reações de apoio dessa viga. Vamos partir dessa seção aí que a gente fez para achar os esforços internos.
Passo 2
Para facilitar, vamos substituir a carga distribuída por uma carga pontual equivalente. O valor delas vai ser a área do retângulo que representa nosso carregamento
E a posição delas é no meio do carregamento distribuído.
O próximo passo é achar as equações do cortante e do momento para a nossa seção. Aí é colocar as representações dos esforços com convenção positiva dentro da nossa seção e usar as equações de equilíbrio para achar os valores desses esforços. Assim:
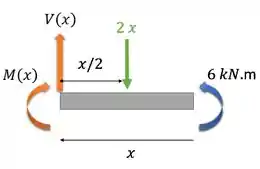
Então agora, vamos calcular o esforço contante e o momento fletor genérico.
Para isso, vamos levar lembrar que a viga tá em equilíbrio assim:
Assim, encontramos que:
E se pegamos o somatório dos momentos na nossa seção, considerando o horário positivo
Assim encontramos o esforço e o momento de forma genérica, sem dar um valor para o .
Essas são as funções que a gente vai usar para fazer os diagramas. Só vamos ter o cuidado de lembrar que nosso sistema de referência começa na extremidade da viga e vai para esquerda.
Passo 3
Podemos achar alguns pontos que vão nos ajudar desenhar nossos diagramas
Mas agora, vamos usar o como :
E o momento:
Vamos tentar , a extremidade da viga
Com esses pontos (e outros que quiser achar) e as funções, a gente consegue fazer os diagramas. Lembrando onde começa e que é uma reta (função linear) e o momento é uma parábola (função do segundo grau) com concavida para baixo.
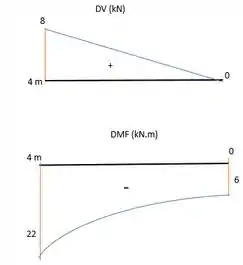
Resposta
