Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 47
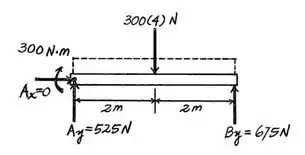
Determine os diagramas de esforço cortante e de momento fletor para a viga simplesmente apoiada.
Passo 1
O problema quer que encontremos o esforço cortante e o momento fletor.
Então observando rapidamente, podemos notar que o corpo encontra-se em equilíbrio, então a gente vai usar a equação de equilíbrio, pois a soma das forças e dos momentos são .
Mas vamos logo calcular as forças de reação em e .
Para isso, vamos considerar o eixo de rotação, assim:
E a força em :
Passo 2
Então agora, usar a equação de equilíbrio:
Na força primeiro:
Assim, encontramos que:
E se pegamos o somatório dos momentos:
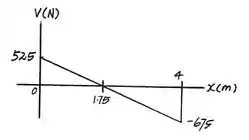
Vamos agora calcula quando o seria :
Passo 3
E por fim valor calcular o momento para :
Resposta
Exercícios de Livros Relacionados
111- Quatro forças atuam numa placa de 700 × 375m m como mostrado na figura. ( a ) Encontre a resultante dessas forças ( b ) Localize os dois pontos onde a linha de ação da resultante intercepta a mar
Para o problema 4.39, a reação em f deve ser para baixo e seu valor máximo admissível deve ser 80 N. Desprezando o atrito nos pinos, determine os intervalor admissíveis para P.
Sabendo que as fendas A e B não possuem atrito e sabendo que P = 60 N , determine (a) a força que cada pino exerce na estrutura e (b) a reação em F.
Determine os diagramas de força cortante e de momento fletor para a viga com a extremidade em balanço.
Determine os diagramas de força cortante e de momento fletor para a viga