Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 40

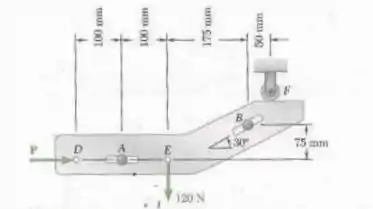
Para o problema 4.39, a reação em f deve ser para baixo e seu valor máximo admissível deve ser 80 N. Desprezando o atrito nos pinos, determine os intervalor admissíveis para P.

Passo 1

Fala aí galera, vamos pra mais um problema de estática. Primeiramente, vamos entender o comportamento da força P. A força P deve ser anulada pela reação horizontal em B, pois é o único ponto que possui reação horizontal. Logo, para que a reação horizontal em B seja a menor possível, a reação vertical nesse ponto deve ser a menor possível também. Para isso, a força em F deve ser a menor possível. Logo, aplicando as equações de equilíbrio:

Logo, resolvendo o sistema:

Logo, a força P será:

Já para o máximo valor de P, basta aplicar a máxima força em F:

Logo:

Portanto, sabemos que:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um componente de máquina é sujeito a forças e binários mostrados na figura. O componente é mantido no local por um único rebite que pode resistir à força, mas não ao binário. Se P = 0 , determine a po

Quando um suporte ajustável B C é usado para aprumar uma parede, o sistema força-binário mostrado na figura é exercido sobre a parede. Substitua esse sistema força-binário por um sistema força-binário

Três crianças estão em pé sobre uma balsa de 5 × 5m . Os pesos das crianças nos pontos A ,B e C são de 375N , 260N e 400N , respectivamente, determine a intensidade e o ponto de aplicação da resultant

Ao utilizar um apontador de lápis, um estudante aplica as forças e o binério mostrado na figura. a Determine as forças exercidas em B e C sabendo que essa forças e o binário são equivalentes a um sist

Para o sistema de exaustão do Problema 3.124. a Substitua o sistema de força por um sistema de força-binário equivalente em F , onde o cano de escape é conectado ao conversor catalítico, b determine s