Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 39
Sabendo que as fendas A e B não possuem atrito e sabendo que determine (a) a força que cada pino exerce na estrutura e (b) a reação em F.
Passo 1
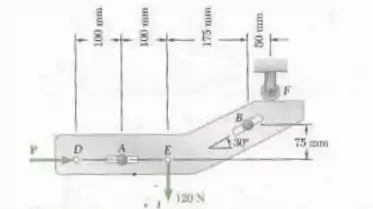
Fala aí galera, vamos pra mais um problema de estática. O primeiro passo é determinar as reações de apoio nos pinos. Para isso, basta aplicar as equações de equilíbrio. Podemos ver que o primeiro pino só restringe o movimento na vertical e o segundo pino possui 2 restrições. Logo:
Agora, utilizando o ângulo dado, devemos determinar a reação na direção y em B:
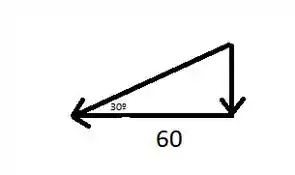
Logo, a reação em y será:
Portanto, a força no pino A deve cancelar as forças para baixo:
Passo 2
Podemos observar que no ponto F não há reação para “sustentar” a estrutura, mas somente para impedir que ela gire. Logo, para determinar a reação em F, vamos aplicar o somatório de momento em algum ponto:
Logo, esta é a força que deverá atuar em F para que a estrutura não gire (esteja em equilíbrio).