Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 42
Determine os diagramas de esforço cortante e de momento fletor para a viga. Todas as polias têm um raio de . Despreze o peso da viga e da montagem das polias. A esfera pesa .
Passo 1
Cara, primeiro vamos entender o que está acontecendo ali. Temos polias e uma corda passando por elas. A parada é que a polia trasmite a tensão na corda para a viga.
Nós sabemos que a tensão em uma corda é igual por todas as partes dela, e se olharmos bem para o problema, o que este causando a tensão na corda é o peso de .
Desse modo, a gente tem que a viga sofre uma força para baixo na direção dessa extremidade dessa corda. E tabém uma força horizontal na direção da outra extremidade. Olha num esqueminha:
Como ele diz para a gente dispensar os efeitos das montagens da polia, a gente não precisa levar em consideração essas forcinhas de , que são resultantes das tensões da corda cobre cada polia ali.
Levando em consideração o raio da polia para localizar as forças que a gente vai considerar (as azuis e as de reação), temos um DCL assim:
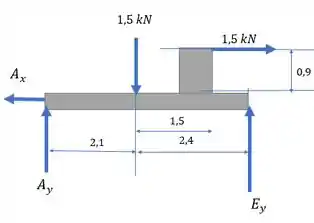
O problema quer que a gente encontre o diagrama de esforço cortante e de momento fletor. Então vamos começar achando as reações em e , e depois fazendo as equações do momento e do cortante
Passo 2
Então agora, vamos calcular as reações de apoio, para isso vamos considerar como o eixo de rotação, sabendo que o momento deve ser , porque o corpo está em equilíbrio, né?
Assim, encontramos que:
E se pegamos o somatório das forças verticais:
Assim encontramos as reações dos dois apoios.
E pelo equilíbrio na direção .
Passo 3
Agora vamos achar os diagramas. A gente vai dividir nossa viga em 3 regiões, porque temos duas forças concentradas agindo nela.
Vamos fazer seções genéricas em cada uma dessas regiões, olhar só para a esquerda, posicionar o momento e cortante na orientação positva e achar as equações para os momentos e cortantes pelo equilíbrio.
Olhando para :
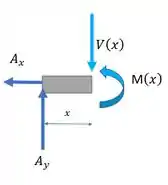
Usando as equações de equilíbrio
Fazendo o somatório de momentos na seção
Passo 4
Fazendo o mesmo para as outras seções:
Para
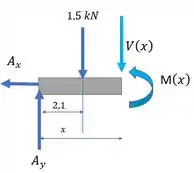
Passo 5
Para , vamos fazer diferente e olhar para a direita da nossa seção. Fica mais tranquilo, assim:
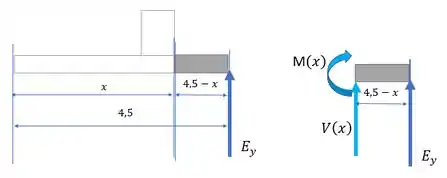
Passo 6
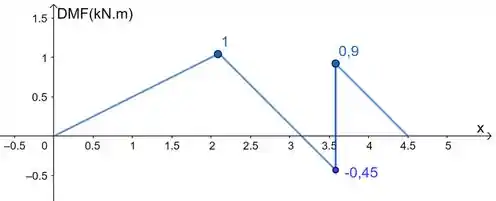
Aí agora é esboçar os gráficos de e respeitando os intervalos:
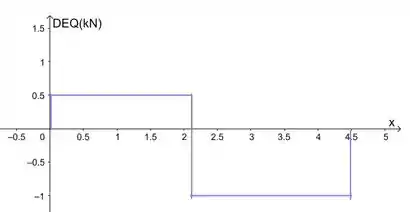
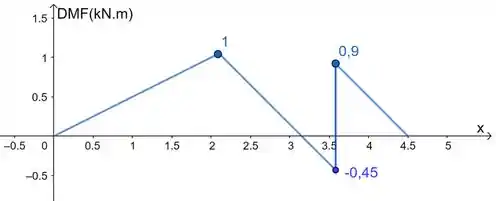
Prontinho!
Obs: Ficou diferente do gabarito, mas estamos certinhos, tá?
Resposta
