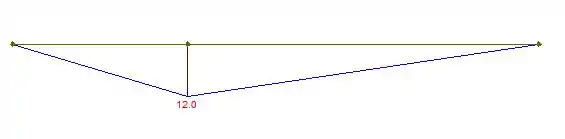
. Determine os diagramas de força cortante e de momento fletor para o eixo em termos dos parâmetros mostrados; considere , , . Há um mancal axial em e um mancal radial em .

Em seguida, utilizar as equações de equilíbrio para determinarmos as reações de apoio:

Para o eixo , temos:

E para o momento, temos:

Logo:

Para determinarmos os esforços cortantes e os momentos fletores para esboçarmos cada diagrama precisamos dividir a nossa viga em porções. Para a primeira, . Pelas equações de equilíbrio, temos:

Para o momento, temos:

Vamos repetir o processo, selecionando a porção restante da viga, ou seja, . Com isso, vamos utilizar as equações de equilíbrio para determinarmos a força cortante e o momento fletor. Temos:

Para o momento, temos:

Agora que determinamos os esforços cortantes e os momentos fletores em cada porção da viga, a gente pode esboçar os diagramas. Primeiro, para a força cortante, temos:

E para o momento fletor, temos:

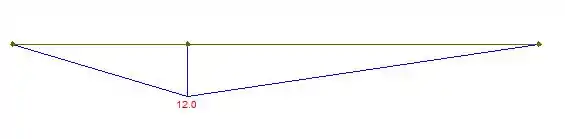
Opa, é isso, galera. Bora praticar mais!!!