Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 85

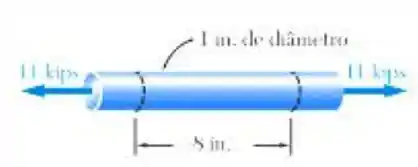
Determine a dilatação e c a variação em volume do segmento de 8in. da barra mostrada se (a) a barra fosse feita de aço com E = 29   x   10 6   p s i     e     v = 0,30   e (b) a barra fosse feita de alumínio com E = 10,6   x   10 6 p s i   e   v = 0,35 .

Passo 1

Fala ai gurizada tudo beleza? O exercício pede para que a gente determine a dilatação e c a variação em volume do segmento de 8in, vamos então determinar a área deste elemento:

A = π 4 d 2 = π 4 1 2 = 0,78540   i n 2 A tensão é dada por:

σ x = P A = 11   x   10 3 0,78540 = 14,0056   x   10 3 p s i

Sabendo que σ y = σ z = 0 e considerando os dados do aço. E = 29   x   10 6   p s i       v = 0,30 vamos determinar a deformação X, Y e Z, então vem comigo :D

ε x = 1 E   x   σ x - v σ y - v σ z = σ x E = 14,0056   x   10 3 29   x   10 6 = 482,95   x   10 6 ε y = 1 E   x   - v σ x + σ y - v σ z = - v σ x E = - v ε x =   - 0,30   x   482,95   x   10 6 = - 144,885   x   10 - 6 ε z = 1 E   x   - v σ x + σ y - v σ z = - v σ x E = ε y = - 144,885   x   10 - 6

Onde: e = ε x + ε y + ε z = 193,2   x   10 - 6

Calculando a variação de volume temos:

∆ v = v e = ∆ L e = 0,78540   x   8   x   193,2   x   10 - 6 = 1,214   x   10 - 3 i n ³

Passo 2

Considerando os dados do alumínio, E = 10,6   x   10 6 p s i       v = 0,35 vamos determinar a deformação X, Y e Z, então vem comigo :D

ε x = σ x E = 14,0056   x   10 3 10,6   x   10 6 = 1,32128   x   10 - 3 ε y = - v ε x =   - 0,35   x   1,32128   x   10 - 3 = - 462,45   x   10 - 6 ε z = ε y = - 462,45   x   10 - 6

Onde:

e = ε x + ε y + ε z = 396   x   10 - 6

Calculando a variação de volume temos:

∆ v = v e = ∆ L e = 0,78540   x   8   x   396   x   10 - 6 = 2,49   x   10 - 3 i n ³

Resposta

  1. 1,214   x   10 - 3 i n ³
  2. 2,49   x   10 - 3 i n ³
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qual a força de P que deverá ser aplicada à placa do problema 2.75 para produzir um deslocamento de 1 16 i n ?
Uma barra de latão AB é envolvida por uma jaqueta utilizada para aplicar uma pressão hidrostática é 40M P a na parte BC de 240 - m m da barra. Sabendo que E = 105G P a e v = 0,33 , determine (a) a var
O bloco mostrado na figura é feito de liga de magnésio com E = 34G P aev = 0,35 . Sabendo que σ x = - 180M P a , determine (a) a intensidade de σ x para qual a qual a variação na altura do bloco será
A placa homogênea ABCD está submetida a um carregamento biaxial como mostra a figura. Sabe-se que σ z = σ 0 e que a variação o comprimento da placa na direção x deve ser zero, ou seja, ϵ x = 0 . Desig
Em muitas situações, sabe-se que a tensão normal em determinada direção é zero, como, σ z = 0 , no caso da placa fina mostrada. Para esse caso, conhecido como estado plano de tensão, mostre que, se as