Em um dado instante, o cilindro tem uma velocidade para baixo de e uma aceleração para cima de . Determine a velocidade e a aceleração correspondentes do cilindro .
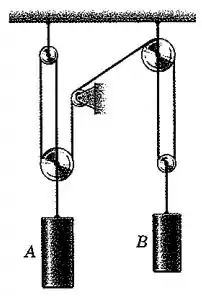
Passo 1
Considere como a distância vertical entre a polia móvel junto ao bloco e a polia fixa na parede, e como a distância entre a polia móvel junto ao bloco e a polia fixa no teto acima de . Temos que o comprimento total da corda é:
Portanto, se derivarmos em relação ao tempo, obteremos:
Então essa é a relação entre as velocidades dos dois blocos. Considerando o sentido para baixo como positivo, obtemos a velocidade do bloco :
Ou seja, o bloco tem uma velocidade de para cima.
Passo 2
Podemos derivar mais uma vez a equação das velocidades para obter a relação entre as acelerações dos dois blocos:
Portanto,
Assim, o bloco tem uma aceleração de para baixo.
Resposta
para cima
para baixo