Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.9 - Ex. 217
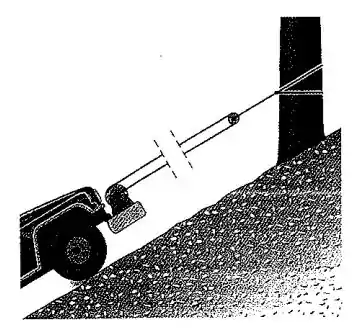
Um caminhão equipado com um guincho motorizado sobre a sua dianteira puxa a si próprio para cima num aclive íngreme com o arranjo de cabo e polia mostrado. Se o cabo é enrolado sobre o tambor na taxa constante de , quanto tempo levará para o caminhão subir do aclive?
Passo 1
Considere como a distância entre os centros das duas polias. Então o comprimento total da porção esticada do cabo é dado por:
Portanto, se derivarmos em relação ao tempo, obteremos:
pois neste caso, o comprimento considerado é variável, com . Portanto:
Logo, a velocidade de subida do caminhão é .
Passo 2
Para calcular o tempo que o caminhão demora para subir , usamos a equação do movimento uniforme:
onde e :
Ou seja, o caminhão demora minutos e segundos para subir .
Resposta
Exercícios de Livros Relacionados
2/121) Despreze os diâmetros das pequenas polias e determine a relação entre a velocidade de A e a velocidade de B para um determinado valor de y .
2/225) Os guinchos motorizados sobre o andaime industrial permitem que este seja elevado ou abaixado . Para a rotação no sentido indicado , o andaime está sendo elevado . Se cada tambor tem um diâmetr
2/1228) Os anéis A e B deslizam ao longo das hastes fizas em ângulo reto e estão conectados por um fio de comprimento L . Determine a aceleração a x do anel B em função de y se o anel A possui uma vel
2/223)Sob aação da força P , aaceleração constante do bloco B é de 2 m / s 2 para cima do plano inclinado . Para o instante em que a velocidade de B é de 1,2m / s subindo o plano inclinado , determine
2/227) A fim de acelerar a elevação dos fardos representados no exemplo 2/16 , o arranjo das polias é alterado como mostrado aqui . Se o trator A tem uma velocidade para a frente v A , determine uma e