Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.9 - Ex. 220
2/120) Para um dado valor de , determine a velocidade ascendente de em termos da velocidade descendente de . Despreze os diâmetros das polias .
Passo 1
Então galera, para resolvermos exercícios desse tipo , devemos primeiramente calcular o comprimento do cabo que aparece na imagem . E para isso , definimos que :
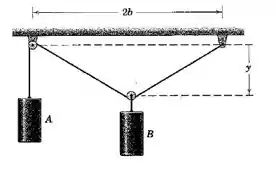
é a distância do centro da polia mais à esquerda até o bloco .
é a distância do teto até o centro da polia que sustenta o bloco .
é a distância que separa as duas polias que estão presas no teto .
Com isso definido , temos que o tamanho do cabo é dado por :
Passo 2
Bom pessoal , agora derivamos para acharmos a velocidade ascendente em :
Além disso , nós sabemos que , . Sendo assim :
Resposta
E aí , topa fazer mais exercícios com a gente?
Exercícios de Livros Relacionados
Se a carga B tem uma velocidade para baixo v B , determine a componente ascendente v A y da velocidade de A em termos de b , do comprimento da haste l e do ângulo θ . Suponha que o cabo que suporta A
O cilindro A tem uma velocidade constante para baixo de 1m / s . Calcule a velocidade do cilindro B para (a) θ = 45 ° , (b) θ = 30 ° , (c) θ = 15 ° . A mola está sob tração durante toda a faixa de int
2/227) A fim de acelerar a elevação dos fardos representados no exemplo 2/16 , o arranjo das polias é alterado como mostrado aqui . Se o trator A tem uma velocidade para a frente v A , determine uma e
2/226) O andaime do Prob.2/225 é modificado aqui pela colocação dos guinhos motorizados no chão em vezde no andaime . As outras condições permanecem as mesmas . Calcule a velocidade de subida v do and
Sob ação da força P , a aceleração constante do bloco B é de 3m / s ² ² para a direita. No instante em que a velocidade de B é de 2m / s para a direita, determine a velocidade de B em relação a A , a