Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.9 - Ex. 218

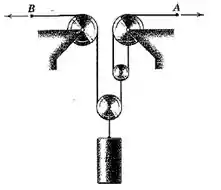
2/118) Para o sistema de polias mostrado , cada um dos cabos em A e B recebe uma velocidade de 2 m / s na direção da seta . Determine a velocidade ascendente v da carga m .

Passo 1

Então galera, para resolvermos exercícios desse tipo , devemos primeiramente calcular o comprimento dos dois cabos que aparecem na imagem . E para isso , definimos que :

x 1 é a distância do centro da polia maior da direita até o ponto A .

x 2   é a distância do centro da polia da esquerda até o ponto B .

y 1 é a distância do centro da polia maior da direita até o centro da polia menor da direita .

y 2 é a distância do centro da polia da esquerda até o centro da polia central .

y 2 - y 1 é a distância do centro da polia menor da direita até o centro da polia central .

Com isso definido , achamos que o comprimento dos cabos é dado por :

c a b o   d a   e s q u e r d a   : x 2 + y 2 + y 2 - y 1 = c o n s t a n t e

c a b o   d a   d i r e i t a   : x 1 + 2 y 1 = 0

Passo 2

Agora devemos derivar cada uma das equações achadas acima para acharmos a velocidade ascendente da carga ( y 2 ' ) :

Derivando a equação do comprimento do cabo da direita :

x 1 ' + 2 y 1 ' = 0

y 1 ' = - x 1 ' 2

Derivando a equação do comprimento do cabo da esquerda :

x 2 ' + 2 y 2 ' - y 1 ' = 0

Passo 3

Bom pessoal , combinando o resultado das duas derivadas , achamos que :

x 2 ' + 2 y 2 ' = - x 1 ' 2 = 0

x 2 ' + 2 y 2 ' + x 1 ' 2 = 0

y 2 ' = - x 2 ' 2 - x 1 ' 4

Como cada um dos cabos em A e B recebe uma velocidade de 2 m / s , temos que :

x 2 ' = x 1 ' = 2 m / s

Sendo assim ,

y 2 ' = - 2 2 - 2 4 = - 1,5   m / s

Resposta

y 2 ' = - 1,5   m / s

Tranquilo pessoal? Então partiu resolver mais questões

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em um dado instante, o cilindro A tem uma velocidade para baixo de 0,8m / s e uma aceleração para cima de 2m / s 2 . Determine a velocidade e a aceleração correspondentes do cilindro B .
Determine a equação de restrição que relaciona as acelerações dos corpos A e B . Assuma que a superfície superior de A permanece na horizontal.
Se o bloco A tem uma velocidade de 0,6m / s para a direita, determine a velocidade do cilindro B .
Se a velocidade x ˙ do bloco A subindo o plano inclinado está aumentando na taxa de 0,044m / s cada segundo, determine a aceleração de B .
2/122) Determine uma expressão para a velocidade v A do carrinho A descendo a inclinação em termos da velocidade de subida v B do cilindro B .