Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 6
Determine as equações da linha elástica para a viga utilizando as coordenadas e . Especifique a deflexão máxima da viga. é costante.
Passo 1
Fala aí pessoal, vamos para mais um exercício de resmat.
Primeiro, vamos determinar as reações de apoio em função do carregamento. Para isso, vamos desenhar DCL e as reações de apoio:
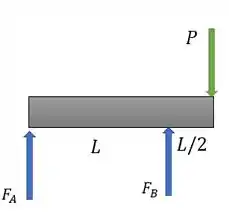
Passo 2
Para determinarmos as forças de reação, vamos utilizar a equação do momento em , temos:
Para a condição no eixo temos:
Passo 3
Com isso, podemos determinar a função de momento fletor. Para .
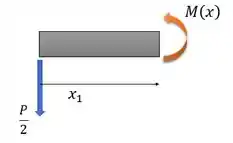
Logo:
E então, pelo método da integração, vamos obter a equação da linha elástica. Fica assim:
Passo 4
Basta repetirmos o processo para :
Integrando:
Passo 5
Para determinarmos as incógnitas restantes, temos que utilizar as seguintes condições de contorno:
Elas mostram que nos apoios, temos deflexão nula.
E também, estas condições de continuidade:
Que mostram que há continuidade de inclinações no ponto .
Substituindo condições de contorno e continuidade:
Resolvendo o sisteminha , achamos:
Passo 6
Com isso, temos as nossas Equações da linha elástica substituindo as reações e constantes encontradas:
Passo 7
A deflexão máxima ou ocorre nos extremos da nossa viga ques estão em balanço ou quando (inclinação nula).
Pela geometria, ocorre no intervalo de . Vamos achar onde:
Isso dá a deflexão:
Vamos calcular a deflexão na extremidade com balanço para comparar:
E assim, a deflexão máxima ocorre em , e vale: