Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 3.Problemas - Ex. 13
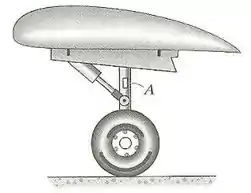
A mudança de peso de um avião é determinada pela leitura de um extensômetro A montado no suporte de alumínio da roda do avião. Antes de o avião ser carregado, a leitura do extensômetro no suporte é , ao passo que, após o carregamento, é . Determine a mudança na força que age sobre o suporte se a área da seção transversal dele for . .
Passo 1
Fala aí pessoal, bora para mais um exercício de resmat. Este problema nos pede para acharmos a mudança na força que age sobre o suporte, dado que a área da seção transversal.
Ou seja, se inicialmente a gente tinha uma força atuando e depois uma força atuando, a gente quer
E ele dá as deformações em cada um desses momentos. Vamos usar essas deformações e outros dados que ele dá para achar essa variação aí. Bora!
Passo 2
Então, a gente pode achar uma expressão para a força através da exprssão da tensão. A expressão da tensão é
A área da seção tranversal não muda no nosso caso, apenas a força . Então em cada caso teremos uma tensão com valor diferente. No caso inicial, vamos ter
E para o caso final:
Vamos substituir essas coisas na expressão da nossa variação:
Passo 3
Como ele deu a deformação em cada momento, vamos usar a lei de Hooke para achar expressões para essas tensões, supondo que a gente sempre está no regime elástico:
Para o caso inicial, temos e a deformação é , então
Já para o caso final, temos e a deformação é , então
Substituindo na nossa expressão para a variação da força:
Passo 4
A nossa área vale , substituindo na nossa expressão e calculando:
Passando essa área para metros quadrados e fazendo as continhas, vamos achar:
Prontoooo!!!!!!!