Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 3.Problemas - Ex. 16
O poste é sustentado por um pino em C e por um arame de ancoragem AB de aço . Se o diâmetro do arame for , determine quanto ele se deforma quando uma força horizontal de agir sobre o poste.
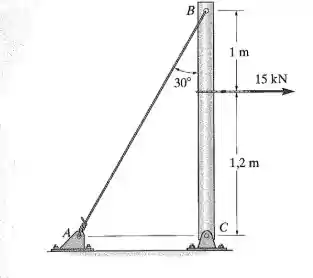
Passo 1
Primeiro, vamos determinar a tração no cabo:
O comprimento do cabo será:
Passo 2
Agora, podemos calcular a tensão:
Utilizando o módulo de elasticidade do aço, podemos determinar a deformação:
Logo, podemos calcular quanto o cabo se deforma:
Resposta
Exercícios de Livros Relacionados
Nós expressamos por ε 1 , ε 2 e ε 3 as três medidas de deformação específica normal feitas com uma roseta à 60°. Pede-se (b) Sabendo-se que as seguintes medidas foram feitas com esta roseta, em um dad
Nós expressamos por ε 1 , ε 2 e ε 3 as três medidas de deformação específica normal feitas com uma roseta à 60°. Pede-se (a) mostrar que a soma destas deformações e a soma do quadrado de suas diferenç
O círculo de Mohr mostrado corresponde ao estado de tensões dado nas Figs. 6.5a e b, Sec. 6.1. Notando que σ x ' = O C ' - C X ' cos 2 θ p - 2 θ e que τ x ' y ' = C X ' s e n ( 2 θ p - 2 θ ) , desen
Sabendo-se que o diâmetro da barra de aço A B D é 30m m , determinar (a) os planos principais; (b) as tensões principais; (c) a máxima tensão de cisalhamento, no ponto H .
O tanque de ar comprimido AB tem um diâmetro externo de 462 m m e uma espessura uniforme e 6 m m . Sabendo-se que a pressão dentro do vaso é de 130k P a , determinar a máxima tensão normal e a máxima