Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas de Revisão - Ex. 152

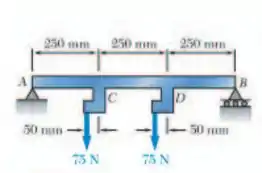
Trace os diagramas de força cortante e momento fletor para a viga e o carregamento mostrados e determine e determine o valor máximo absoluto ( a ) da força cortante e ( b ) do momento fletor.

Passo 1

Fala aí, galerinha. Tudo bem com vocês? Bora estudar mecânica e garantir aquele notão na prova.

Este problema nos pede para determinarmos a tensão máxima em razão da flexão. Para isso, precisamos determinar os diagramas para o momento fletor e força cortante. Primeiro, vamos esboçar o DCL:

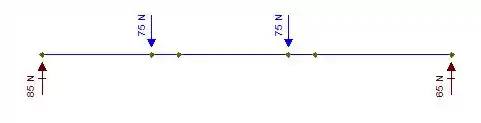
Para acharmos as reações, vamos utilizar as equações de equilíbrio. Sabemos que:

∑ M B = 0 0,75 F A + 0,550 75 + 0,3 75 = 0 F A = 85   N F B = 65   N

Com isso, podemos esboçar os diagramas. Para o diagrama da força cortente:

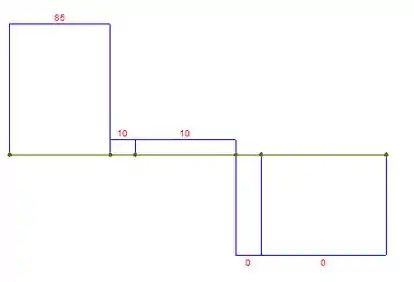
Podemos ver que a força cortante máxima absoluta é V m á x = 85   N .

Passo 2

Agora que já temos o força cortante, vamos para o momento fletor máximo absoluto. Pegaremos o segmento C D , e calcularemos o momento à direita do ponto D , temos:

∑ M D = 0 M - 0,25 85 = 0 M = 21,25   N ∙ m

E pronto! Esta é o máximo momento fletor absoluto. A gente pode conferir o resultado calculando os momentos nos demais pontos.

Resposta

V m á x = 85   N

M = 21,25   N ∙ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga tem a seção transversal mostrada na figura. Se for feita de aço com tensão admissível σ a d m = 170M P a , determine o maior momento interno ao qual ela pode resistir se o momento for aplicado
A peça de mármore, que podemos considerar como um material linear elástico frágil, tem peso específico de 24k N / m ³ ³ e espessura de 20m m . Calcule a tensão de flexão máxima na peça se ela estiver
A peça de mármore, que podemos considerar como um material linear elástico frágil, tem peso específico de 24k N / m ³ ³ e espessura de 20m m . Calcule a tensão de flexão máxima na peça se ela estiver
Foram apresentadas duas alternativas para o projeto de uma viga. Determine qual delas suportará um momento de M=150k N·m com a menor quantidade de tensão de flexão. Qual é essa tensão? Com que porcent
O elemento tem seção transversal com as dimensões mostradas na figura. Determine o maior momento M que pode ser aplicado sem ultrapassar as tensões de tração e compressão admissíveis de (σt)adm = 150