Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 60

Determine o posicionamento a do apoio de rolete B de modo que o momento fletor máximo dentro do trecho A B seja equivalente ao momento fletor no apoio B .

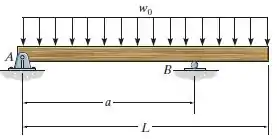
Passo 1

Vamos desenhar o diagrama de corpo livre da viga, beleza?

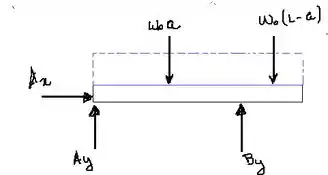
Antes de encontrarmos os valores do esforço cortante e momento fletor, vamos encontrar as reações de apoio através do diagrama de corpo livre desenhada acima. Assim,

∑ M A = 0

w o a a 2 - B y a + w o L - a L - a 2 + a = 0

w o a 2 2 - B y a + w o L - a L + a 2 = 0

B y a = w o 2 a 2 + L 2 - a 2 = 0

B y = w o L 2 2 a

∑ F y = 0

A y + B y - w o a - w o ( L - a ) = 0

A y = w o a + w o L - a - w o L 2 2 a

A y = w o 2 a 2 + 2 a L - 2 a 2 - L 2 2 a

A y = w o 2 a [ 2 a L - L 2 ]

Passo 2

Vamos agora olhar para a porção que compreende o intervalor 0 ≤ x ≤ a . Vamos aplicar as equações de equilíbrio no diagrama de corpo libre para determinarmos a força cortante V e o momento fletor M .

∑ F y = 0

- V - w o x + A y = 0

V = w o x - w o 2 a [ 2 a L - L 2 ]

V 0 - a = w o 2 a 2 a L - L 2 - 2 a x

∑ M = 0

M + w o x x 2 - A y x = 0

M = w o 2 a 2 a L - L 2 x - w o x 2 2

M 0 - a = w o 2 a 2 a L - L 2 x - a x 2

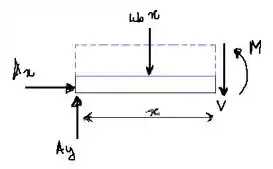
Passo 3

Vamos agora olhar para a porção que compreende o intervalor a ≤ x ≤ L . Vamos aplicar as equações de equilíbrio no diagrama de corpo libre para determinarmos a força cortante V e o momento fletor M .

∑ F y = 0

- V - w o ( L - x ) = 0

V a - L = w o ( L - x )

∑ M = 0

- M - w o L - x 1 2 L - x = 0

M a - L = - w o 2 L - x 2

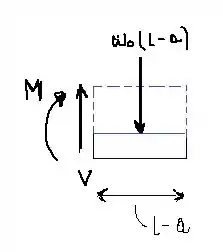
Passo 4

O local em que temos o esforço cortante é igual a zero pode ser obtido fazendo V = 0 . Assim:

0 = w o 2 a ( 2 a L - L 2 - 2 a x )

x = 2 a L - L 2 2 a

Em consequência, o momento máximo ocorre no local onde V = 0 . Vamos substituir o valor de x na expressão do momento!

M m a x = w o 2 a 2 a L - L 2 2 a L - L 2 2 a - a 2 a L - L 2 2 a 2

M m a x = w o 8 a 2 2 a L - L 2 2

Passo 5

O momento de suporte em B pode ser calculado fazendo x = a . Assim,

M s u p o r t e = w o 2 a 2 a L - L 2 a - a 3

M s u p o r t e = w o 2 2 a L - L 2 - a 2

M s u p o r t e = - w o 2 L - a 2

Passo 6

Como precisamos que M m a x = M s u p o r t e , temos:

w o 8 a 2 2 a L - L 2 2 = w o 2 L - a 2

a = L 2

Resposta

O valor de a é igual a:

a = L 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se L = 5,4m , a viga falhará quando a força cortante máxima for V m á x = 4k N á ou o momento fletor máximo for M m á x = 1,8k N ⋅ m á . Determine a maior intensidade w da carga distribuida que ela su
O frustum do cone está em balanço a partir do ponto A . Se o cone é feito de um material tendo peso específico de γ , determine a força cortante e o momento fletor interno no cone como uma função de x
Determine a tração em cada segmento do cabo, e do comprimento total do cabo. Faça P = 400N .
Se cada segmento do cabo puder suportar uma tração máxima de 375N , determine a maior carga P que pode ser aplicada.
O cabo A B C D suporta a lâmpada E de 10k g e a lâmpada F de 15k g . Determine a tração máxima no cabo e a flecha y B do ponto B .