Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 19
Determine as forças normal e cortante e o momento fletor nos pontos e da viga composta por três elementos. O ponto está localizado logo à esquerda da força de .
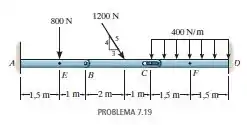
Passo 1
Falaa galerinha. Beleza??
Nessa questão vamos precisar usar os conceitos de estática de praxe:
- Somatório das forças em :
- Somatório das forças em :
- Momento:
E vamos usar uma tática diferente de fazer primeiro o diagrama de corpo livre tooooodo e depois ir cortando.
Repara que queremos SOMENTE as forças e os momentos nos pontos e . Então pode ser interessante a gente pegar pedaços pequenos tipo e , né??
Pra isso vamos precisar das reações de apoio nesses pinos em e . Então vamos começar dividindo só nesse pedacinho.
Passo 2
Dividindo no segmento
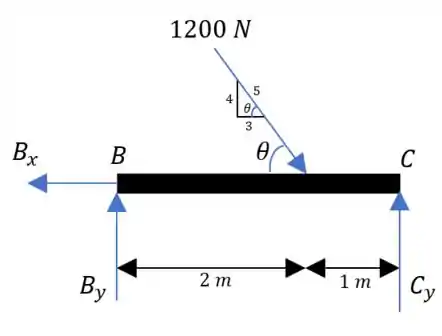
Fazendo o somatório das forças em :
E das forças em :
E o balanço de momento em :
Daí, então:
Passo 3
Agora sim vamos achar o que realmente a questão está pedindo...
Para o segmento
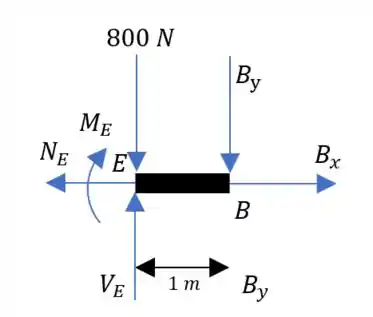
Fazendo o somatório das forças em
O somatório das forças em :
E para o momento:
Pra esse ponto já foi... Bora pro ponto , então...
Passo 4
Para o segmento :
Lembrando que a carga distribuída a gente pode substituir por uma pontual equivalente e colocar ela bem no meio, ok??
Fazendo o somatório das forças em :
Em :
E para o momento:
Ufaa... essa deu trabalho, né? Mas acabou. Bora pra próxima...