Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 16
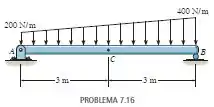
Determine as forças normal e cortante e o momento fletor no ponto da viga.
Passo 1
Fala aí... beleza???
Nessa questão vamos precisar dos conceitos de estática:
- O somatório das forças em é igual a zero:
- O somatório das forças em é igual a zero:
- O somatório dos momentos também é igual a zero:
Já vamos começar fazendo o diagrama de corpo livre:
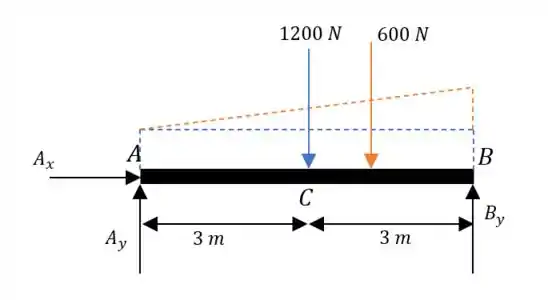
Podemos dividir a carga distribuída em duas partes. Uma retangular:
E uma triangular (lembrando que essa não fica na metade barra, mas sim a 1/3 de onde está a parte maior do triângulo):
Passo 2
Fazendo o somatório das forças em :
Das forças em :
Para o momento:
Passo 3
Agora vamos dividir a barra no ponto :
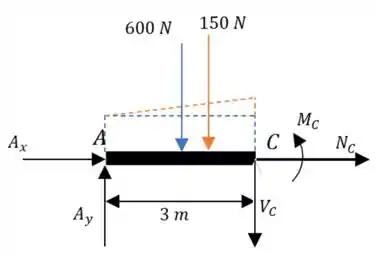
Lembrando que precisamos recalcular a carga distribuída porque agora é só um pedaço, heim...
- Para a retangular:
- Para a triangular:
Fazendo o somatório das forças em :
Em :
E para o momento:
Prontinho... Essa já foi. Bora pra próxima??