Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 127

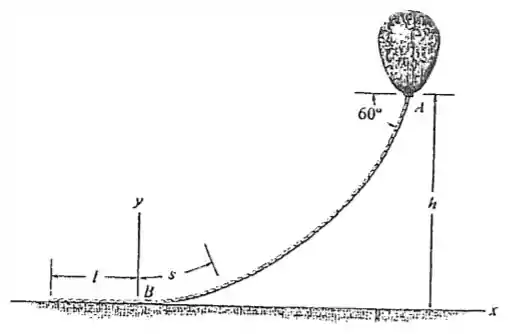
O balão é mantido no lugar usando uma corda de 120 m que pesa 16 N / m e faz um ângulo de 60 ° com a horizontal. Se a tração na corda no ponto A   é 750 N , determine o comprimente da corda, l , que está encostada no solo, e a altura h . Dica: Estabeleça o sistema de coordenadas em B , como mostra a figura.

Passo 1

Desejamos encontrar o valor da altura h e o comprimento do cabo ( l ) . A curva de deflexão do cabo vai ser dada por

x = ∫ d s 1 + 1 F h 2 ⋅ ∫ w 0 d s 2 1 2  

Quando w 0 = 16 N m . Agora, podemos utilizar a fórmula

x = F h w 0 ⋅ sinh - 1 ⁡ 1 F h ⋅ w 0 ⋅ s + C 1 + C 2      

x = F h 16 ⋅ sinh - 1 ⁡ 1 F h ⋅ 16 ⋅ s + C 1 + C 2         ( i )

Além disso, também temos

d y d x = 1 F h ⋅ ∫ w 0 d s = 1 F h ⋅ 16 s + C 1         ( i i )

Por fim, nossas condições de contorno serão

d y d x = 0   e m   s = 0

Da equação ( i i ) vamos ter C 1 = 0 . Dessa mesma equação vamos ter

d y d x = t a n θ = 16 s F h       ( i i i )

s = 0   e m   x = 0   e   C 1 = 0

→ C 2 = 0   substituindo em ( i ) . Reescrevendo a equação ( i ) em função de s e substituindo em ( i i i ) vamos obter

d y d x = sinh ⁡ 16 F h ⋅ x → y = F H 16 ⋅ cosh ⁡ 16 F h ⋅ x + C 3

Temos que y = 0   e m   x = 0 . Assim → C 3 = - F h 16 .

Passo 2

Por fim, tomemos que a tensão desenvolvida na ponta pregada no balão é de T = 750 N e θ = 60 ° . Então, teremos

T = F h cos ⁡ ( θ ) → F h = 375 N

Da equação ( i i i ) vamos ter

tan ⁡ 60 ° = 16 s 375 → s ≈ 40,6 m  

Logo, o comprimento l da nossa corda será dado por

l = 120 - 40,6 = 79,40 m

Substituindo esses dados em ( i ) vamos obter

x ≈ 37,63 m

Como y = h quando x = 37,63 m vamos ter

h ≈ 28,575 m

Resposta

l = 79,40 m   e   h = 28,575 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as forças normal e cortante e o momento fletor no ponto E .
Determine as forças normal e cortante e o momento fletor em uma seção que passa pelo ponto D . Considere w = 150N / m .
Determine as forças normal e cortante e o momento fletor no ponto D .
Determine as forças normal e cortante e o momento fletor no ponto D da estrutura com dois membros.
Determine as forças normal e cortante e o momento fletor nos pontos C e D da viga simplesmente apoiada. O ponto D está localizado logo à esquerda da carga concentrada de 10k N .